- #1
YoshiMoshi
- 236
- 10
- TL;DR Summary
- Help Adjusting for Toe
It seems that "most" stock sedans do not have adjustable caster, camber and turning angle, provisions are only provided to adjust toe only. I'm trying to find a way to DIY this at home, if this is possible, and had some questions on the theory behind it.
For my car, the stated toe specification for the front is "Front toe-in 0 +/- 2 mm (0+/-0.08 in)", from the service information from the manufacturer.
I see that there are toe plates, that you can purchase to attempt to DIY an alignment.

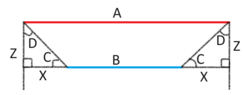
The basic theory in using this tool is that you place the plate up against the wheel, and take two measurements on either side.
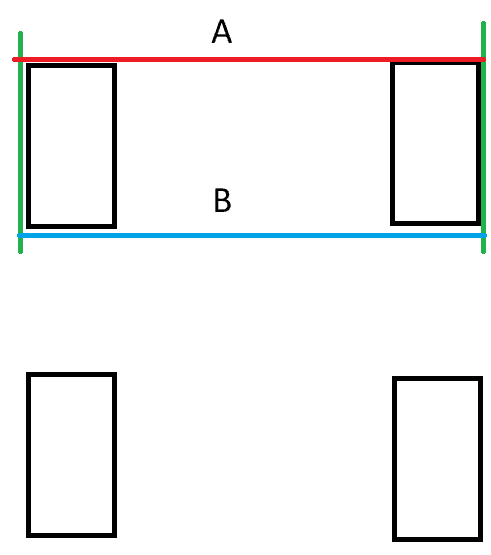
I then subtract the length of line A vs the length of line B. I believe this term is called "Total Toe"?
If( A - B > 0 ){
Toe Out
}
If( A - B < 0 ){
Toe In
}
if( A - B = 0 ){
Neutral Toe
}
This is pretty simple and straight forward.
However is the specified toe "Front toe-in 0 +/- 2 mm (0+/-0.08 in)" the "Total Toe" or the toe for each tire? If this is the toe for each tire, I don't see how to make this adjustment.
I'm not sure that I could just "assume" equal toe of each tire before adjustment. What I mean by this is that the difference between line segment lengths A and B are split evenly on either side of the line segment. In this rough sketch, I labeled both sides "X", indicating that I'm intending them to be the same length. Where abs(A - B)/2 = X
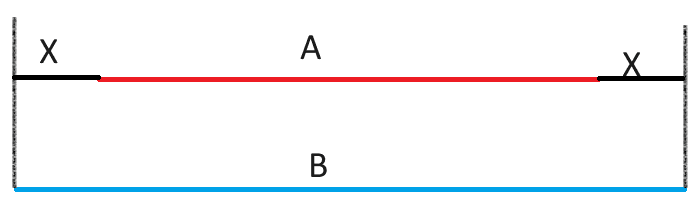
When in reality, I don't see why the difference has to be necessarily equal to each other and I can have this situation, where abs(A - B) gives me some variable Z that is equal to X + Y, and X =/= Y
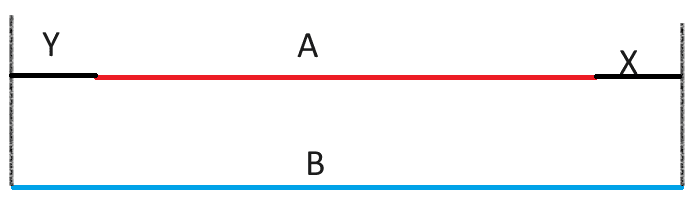
If I could "assume" that the difference is split on either side evenly (which I doubt), I could see how I could do some simple trigonometry to find various angles. Given that the diameter of the tire, Z, is known and specified by the manufacturer of the tire.
In the toe in situation, which angle is the "toe of the tire" C or D?
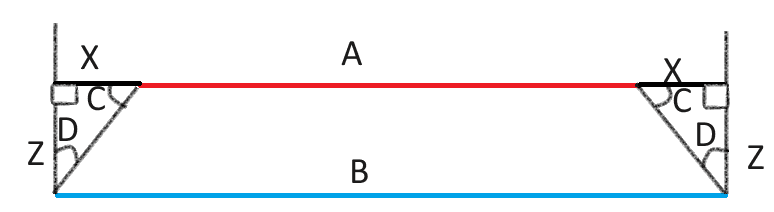
And in the toe out case, which angle is the "toe of the tire" C or D? Exaggerated to allow myself easier time drawing the picture, but you get the point.
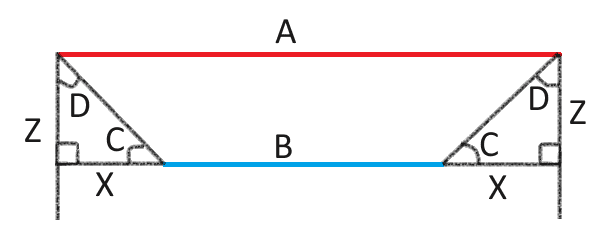
I know how important having a "flat ground" is when doing alignments, but if all your concerned about is the toe, and toe plates is an ok way of calculating toe, then I don't see how working on a driveway that only "appears to be flat" but not may be perfectly flat would matter in measuring the the lengths of line segments A or B. Does the ground really need to be perfectly flat when all I'm worried about is toe?
I know that using these toe plates, does not account for variation in wall thickness of the tire or bulges. But when I have done alignments on an actual alignment rack, the sensors get mounted onto the tires, with arms the clamp down on the outside of the tires. It seems that this is not really something to worry about? I mean you could always remove the tire, brake caliper and rotor, and be left with nothing but the hub. But then you have to consider runout of the wheel hub. It seems like whatever you use to take the measurement is going to have some variation.
I see some manufacturers want you to have a full tank of gas, and alignment racks request that you measure the weight for the amount of "junk" that is in the persons car (provide an estimate), or remove it. Why is this? To me it would make more sense to perform an alignment on an alignment rack with the "normal" amount of weight that is the vehicle. If that means having 100 pounds of "junk", and 400 pounds of people, and a half tank of gas, then why even prompt the technician for this information, or to remove the "junk". Or maybe the owner keeps their car spotless and empty, and only they are in the vehicle. I don't know it just seems odd to me to account for the weight of stuff in the vehicle, as this constantly changes. I get that as you add more weight to the vehicle, the springs will compress, and ride height will decrease, this could effect some of the angles. So then wouldn't you just perform the alignment with whatever is the most common payload for the vehicle, in which case you would just perform the alignment with how the car came to the shop, if that means a spotless car, or a car with 100 pounds of "junk" in it, or even preforming the alignment the customer in the car!
Lastly, I was wondering if you can make adjustments to the outer tie rods and measurements, with the car up in the air on a lift? I do not see how having the car up in the air would change the lengths of line length A and B. Some cars are very low to the ground, and moving the outer tie rods and re-measuring is impossible with the car fully on the ground. It would be easier to jack it up a little bit, or have it on a lift and the suspension unloaded.
Thanks for any help in understanding toe alignment theory and nomenclature.
For my car, the stated toe specification for the front is "Front toe-in 0 +/- 2 mm (0+/-0.08 in)", from the service information from the manufacturer.
I see that there are toe plates, that you can purchase to attempt to DIY an alignment.
The basic theory in using this tool is that you place the plate up against the wheel, and take two measurements on either side.
I then subtract the length of line A vs the length of line B. I believe this term is called "Total Toe"?
If( A - B > 0 ){
Toe Out
}
If( A - B < 0 ){
Toe In
}
if( A - B = 0 ){
Neutral Toe
}
This is pretty simple and straight forward.
However is the specified toe "Front toe-in 0 +/- 2 mm (0+/-0.08 in)" the "Total Toe" or the toe for each tire? If this is the toe for each tire, I don't see how to make this adjustment.
I'm not sure that I could just "assume" equal toe of each tire before adjustment. What I mean by this is that the difference between line segment lengths A and B are split evenly on either side of the line segment. In this rough sketch, I labeled both sides "X", indicating that I'm intending them to be the same length. Where abs(A - B)/2 = X
When in reality, I don't see why the difference has to be necessarily equal to each other and I can have this situation, where abs(A - B) gives me some variable Z that is equal to X + Y, and X =/= Y
If I could "assume" that the difference is split on either side evenly (which I doubt), I could see how I could do some simple trigonometry to find various angles. Given that the diameter of the tire, Z, is known and specified by the manufacturer of the tire.
In the toe in situation, which angle is the "toe of the tire" C or D?
And in the toe out case, which angle is the "toe of the tire" C or D? Exaggerated to allow myself easier time drawing the picture, but you get the point.
I know how important having a "flat ground" is when doing alignments, but if all your concerned about is the toe, and toe plates is an ok way of calculating toe, then I don't see how working on a driveway that only "appears to be flat" but not may be perfectly flat would matter in measuring the the lengths of line segments A or B. Does the ground really need to be perfectly flat when all I'm worried about is toe?
I know that using these toe plates, does not account for variation in wall thickness of the tire or bulges. But when I have done alignments on an actual alignment rack, the sensors get mounted onto the tires, with arms the clamp down on the outside of the tires. It seems that this is not really something to worry about? I mean you could always remove the tire, brake caliper and rotor, and be left with nothing but the hub. But then you have to consider runout of the wheel hub. It seems like whatever you use to take the measurement is going to have some variation.
I see some manufacturers want you to have a full tank of gas, and alignment racks request that you measure the weight for the amount of "junk" that is in the persons car (provide an estimate), or remove it. Why is this? To me it would make more sense to perform an alignment on an alignment rack with the "normal" amount of weight that is the vehicle. If that means having 100 pounds of "junk", and 400 pounds of people, and a half tank of gas, then why even prompt the technician for this information, or to remove the "junk". Or maybe the owner keeps their car spotless and empty, and only they are in the vehicle. I don't know it just seems odd to me to account for the weight of stuff in the vehicle, as this constantly changes. I get that as you add more weight to the vehicle, the springs will compress, and ride height will decrease, this could effect some of the angles. So then wouldn't you just perform the alignment with whatever is the most common payload for the vehicle, in which case you would just perform the alignment with how the car came to the shop, if that means a spotless car, or a car with 100 pounds of "junk" in it, or even preforming the alignment the customer in the car!
Lastly, I was wondering if you can make adjustments to the outer tie rods and measurements, with the car up in the air on a lift? I do not see how having the car up in the air would change the lengths of line length A and B. Some cars are very low to the ground, and moving the outer tie rods and re-measuring is impossible with the car fully on the ground. It would be easier to jack it up a little bit, or have it on a lift and the suspension unloaded.
Thanks for any help in understanding toe alignment theory and nomenclature.