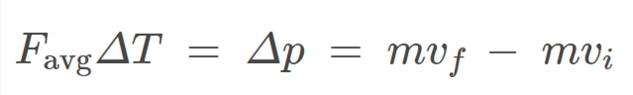Average force when a bouncy ball collides with surface

[String theory guy]

Homework Statement

The statement is below.

Relevant Equations

Impulse is the time integral of force which is equal to the product of the average force with the change in time

What have mistakes/wrong assumption have I made in solving this question?

I tried to solve the problem this way

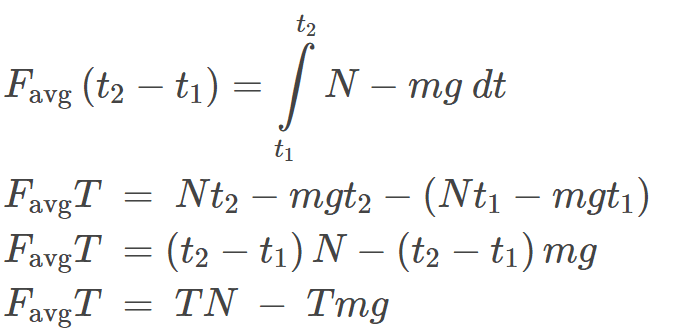
N.B. I assume that the j hat direction is up.

 

[kuruman]

First off you should put parentheses where they belong. So the starting equation should be
$$F_{\text{avg}}(t_2-t_1)=\int_{t_1}^{t_2}(N-mg)dt.$$ Missing parentheses is not a serious mistake. A more serious mistake is in the next line. Note that in the integrand $mg$ is constant, but the normal force $N$ is not and cannot be taken out of the integral, unless you meant to write $N_{\text{avg}}$ and not $N$. Also, you need to figure out how to use the information that the ball starts at $h_i$ and bounces back up to $h_{\!f}$. How do you think you could do that?

 

[String theory guy]

First off you should put parentheses where they belong. So the starting equation should be
$$F_{\text{avg}}(t_2-t_1)=\int_{t_1}^{t_2}(N-mg)dt.$$ Missing parentheses is not a serious mistake. A more serious mistake is in the next line. Note that in the integrand $mg$ is constant, but the normal force $N$ is not and cannot be taken out of the integral, unless you meant to write $N_{\text{avg}}$ and not $N$. Also, you need to figure out how to use the information that the ball starts at $h_i$ and bounces back up to $h_{\!f}$. How do you think you could do that?

I would use the kinematic formulae I think. I guess yo added the parentheses since the differential time is multiped to both force functions.

How would you take -mg out of the integrand since it is not multiped to to the N @kuruman ?

 

[kuruman]

How would you take -mg out of the integrand since it is not multiped to to the N @kuruman ?

It is better to start from the definition of the average force $$F_{\text{avg}}=\frac{\int_{t_1}^{t_2}(N-mg)dt}{\int_{t_1}^{t_2}dt}=\frac{\int_{t_1}^{t_2}Ndt}{\int_{t_1}^{t_2}dt}-\frac{\int_{t_1}^{t_2}mg~dt}{\int_{t_1}^{t_2}dt}=N_{\text{avg}}-mg.$$ You don't need the time interval $T$.

 

[String theory guy]

It is better to start from the definition of the average force $$F_{\text{avg}}=\frac{\int_{t_1}^{t_2}(N-mg)dt}{\int_{t_1}^{t_2}dt}=\frac{\int_{t_1}^{t_2}Ndt}{\int_{t_1}^{t_2}dt}-\frac{\int_{t_1}^{t_2}mg~dt}{\int_{t_1}^{t_2}dt}=N_{\text{avg}}-mg.$$ You don't need the time interval $T$.

Oh so my working at the top actually got the same average force expression as you. Thought, somehow we got to get would of force avg @kuruman .

 

[kuruman]

Oh so my working at the top actually got the same average force expression as you.

It did not. Your expression has $N$ not $N_{\text{avg}}$. The two are not the same. You did not take an average, I did and showed you how it's done. So how will you proceed to find $N_{\text{avg}}$?

 

[haruspex]

There is a slight ambiguity in the question. It should specify that the time average is to be over the duration of the contact, not of the whole process.
Since it starts and ends with the ball stationary, the time average over the whole process is mg. That gives a way to find the average over the contact period, other than the more obvious way.

 

[String theory guy]

It did not. Your expression has $N$ not $N_{\text{avg}}$. The two are not the same. You did not take an average, I did and showed you how it's done. So how will you proceed to find $N_{\text{avg}}$?

Um well, I tried rearranging but now I need to get rid of the average force @kuruman .

 

[haruspex]

Um well, I tried rearranging but now I need to get rid of the average force @kuruman .
View attachment 318937

You have not attempted to use the heights information.

 

[String theory guy]

You have not attempted to use the heights information.

So I think to attempt to use the heights information I could use the kinematic formulae. However, I'm not sure how to relate the initial and finial heights to the force average. That's the issue.

 

[PeroK]

So I think to attempt to use the heights information I could use the kinematic formulae. However, I'm not sure how to relate the initial and finial heights to the force average. That's the issue.

It seems to me that you have missed the point entirely. You have no information about the force profile during the collision, so there is no point integrating the force at all.

What do the initial and final heights tell you in terms of physical quantities?

 

[PeroK]

Hint. Assume $h_f =0$. How would you solve the problem then?

 

[erobz]

So I think to attempt to use the heights information I could use the kinematic formulae. However, I'm not sure how to relate the initial and finial heights to the force average. That's the issue.

I think you are forgetting about the "other half" of the Impulse\Momentum definition.

 

[Steve4Physics]

Let me say the words that others dare not speak...

Impulse = change of momentum​

 

[String theory guy]

Hint. Assume $h_f =0$. How would you solve the problem then?

Ah. Thinking.

 

[Steve4Physics]

Ah. Thinking.

Hi @String theory guy. Since you are still working on this, and ‘tis the season of goodwill (for some), here is another hint.

Using $h_i$, can you work out the velocity of the ball immediately before the bounce (i.e. immediately before initial contact of the ball and the surface)?

Using $h_f$, can you work out the velocity of the ball immediately after the bounce (i.e. immediately after loss of contact between the ball and the surface)?

Can you now use this information? (if you can’t, re-read the posts).

 

[neilparker62]

There is a slight ambiguity in the question. It should specify that the time average is to be over the duration of the contact, not of the whole process.
Since it starts and ends with the ball stationary, the time average over the whole process is mg. That gives a way to find the average over the contact period, other than the more obvious way.

It did say that the ball is in contact with the table for time T and T is supposed to be in the expression you come up with. As indicated by others we just need to calculate $\frac {\Delta p}{\Delta t}$ with the denominator being T.

 

[haruspex]

and T is supposed to be in the expression you come up with.

No, T is one of a long list allowed to be in the expression.

 

[neilparker62]

It was anyway important to make the point you made about working with time average during contact time.

 

[String theory guy]

Can someone write their solution to this problem?

 

[neilparker62]

Can someone write their solution to this problem?

Ideally "someone" should be yourself! I think there are enough hints above for you to write an expression for the change in momentum $\Delta p$. Then simply divide by contact time $\Delta t$.

 

[String theory guy]

It did say that the ball is in contact with the table for time T and T is supposed to be in the expression you come up with. As indicated by others we just need to calculate $\frac {\Delta p}{\Delta t}$ with the denominator being T.

Thanks you

 

[haruspex]

Thanks you
View attachment 320738
View attachment 320739
View attachment 320740

Ok, if I guess correctly how you are defining $v_f, v_i$. But those are not allowed in the answer. So how to get rid of them?

 

[String theory guy]

Ok, if I guess correctly how you are defining $v_f, v_i$. But those are not allowed in the answer. So how to get rid of them?

Thanks, I see how they got their result now.