Average path length through a box

[jamie.j1989]

Hi, I would like to try and calculate the average distance traveled through a box of length $w$ by any straight path possible. As shown in the attached figure. Where the path through the box to an adjacent face is given by

$$r_{adj}^2=\left(\frac{w}{2}-x\right)^2+y^2+z^2.$$

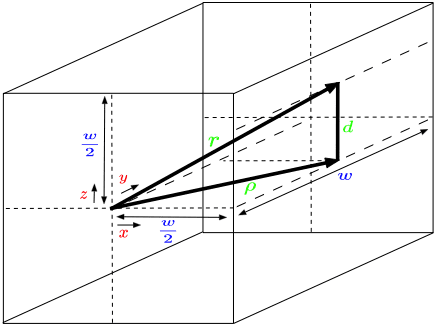
The average distance traveled through the intersection can be found by integrating over the three spatial dimensions $x,y,$ and $z$, in the following way,$$\left<r_{adj}\right>=\frac{1}{N_xN_yN_z}\sum^{N_x,N_y,N_z}_{i,j,k}\sqrt{\left(\frac{w}{2}-x_i\right)^2+y_j^2+z_k^2}$$Where $N_x=\frac{w}{\delta x},N_y=\frac{w}{\delta y},N_z=\frac{w}{\delta z}$, the small change in displacement along $x$ is $\delta x=x_{i}-x_{i-1}$, and likewise for $\delta y$ and $\delta z$. And as $N_x,N_y,N_z\rightarrow \infty$, the summation turns into the integration,

$$\left<r_{adj}\right>=\frac{1}{w^3}\int^{\frac{w}{2}}_{-\frac{w}{2}}dx\int^{w}_{0}dy\int^{\frac{w}{2}}_{-\frac{w}{2}}dz\sqrt{\left(\frac{w}{2}-x\right)^2+y^2+z^2}.$$

So this then gives us the average distance through the box traveled between one adjacent face and the other. All other similar paths with adjacent faces will add and average to the same value.

Then we need to consider paths to opposite faces through the box, where the second figure attached shows the path taken, and where the distance traveled is,

$$r_{opp} =\sqrt{\left(\frac{w}{2}-x\right)^2+w^2+\left(\frac{w}{2}-z\right)^2}$$

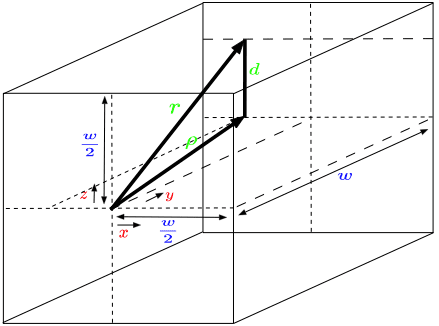
And so we can average like before to get,

$$\left<r_{opp}\right> = \frac{1}{w^2}\int^{\frac{w}{2}}_{-\frac{w}{2}}dx\int^{\frac{w}{2}}_{-\frac{w}{2}}dz\sqrt{\left(\frac{w}{2}-x\right)^2+w^2+\left(\frac{w}{2}-z\right)^2}$$

Where all other paths originating from all other faces and going to their respective opposite faces will just average to the same again. And now the total average is just

$$\left<r\right>=\frac{\left<r_{opp}\right>+\left<r_{adj}\right>}{2}$$

I'm not really sure if this is right, and apart from writing a simulation to compute and average over many possible path lengths I'm not sure how to check it either?

Thanks

 

[haruspex]

I would have thought the idea was to have all directions equally likely, so long as they go through the box.
Using Cartesian coordinates related to the exit points will not achieve that. It will make the oblique angles more common than is fair.
Also, I'm not quite sure what range of entry points is to be considered. The diagram implies it is always through the centre of one end of the box. Is that right?

 

[BvU]

Hi guys,
The situation described reminded me of the view factor in radiative heat transfer. Page 9 http://www.kostic.niu.edu/352/_352-posted/Heat_4e_Chap13-Radiation_HT_lecture-PDF.pdf demonstrates how hideous the resulting expressions are. I expect something equally labyrinthic for the average path lengths ! Things simplify considerably if the single entry point is the center of one of the faces, but an elegant, simple expression is too much to hope for is my humble guess.

 

[mfb]

First you have to define what you want to average over. Over the possible exit area, over the solid angle, over something else?

Is your initial entry point fixed?

 

[jamie.j1989]

First you have to define what you want to average over. Over the possible exit area, over the solid angle, over something else?

Is your initial entry point fixed?

The average is over the distance of the path traveled through the box in a straight line. The entry point isn't fixed, now that the fixed entry point has been mentioned I realize that this isn't correct. I would need 6 degrees of freedom to explain all the possible entry and exit points?

 

[jamie.j1989]

I would have thought the idea was to have all directions equally likely, so long as they go through the box.
Using Cartesian coordinates related to the exit points will not achieve that. It will make the oblique angles more common than is fair.
Also, I'm not quite sure what range of entry points is to be considered. The diagram implies it is always through the centre of one end of the box. Is that right?

I'm not sure I understand, why would the oblique angles be more common?

 

[haruspex]

I'm not sure I understand, why would the oblique angles be more common?

It might be clearer to start with two dimensions.
Consider straight lines through the origin traversing the unit square in the first quadrant.
By symmetry, only need to consider those passing below (1,1).
If we take the y intercept at x=1 as being uniformly distributed, the probability of the intercept being between y and y+dy is dy. If the angle to the horizontal is θ, the probability of the angle being between θ and θ+dθ is sec²(θ)dθ.
If you want all angles equally likely, you need the probability to be (4/π)dθ.

 

[mfb]

The average is over the distance of the path traveled through the box in a straight line.

That is what you average, it is not what you average over.

As an example, consider a die which has faces "1", "1", "4", "4", "4", "4". What is the average? You can average over the result of many rolls: 3. But you can also average over the possible results (1 and 4): 2.5. This example might look a bit constructed, but you have exactly this problem with your cube: It is unclear how to weight the different possible results relative to each other. By surface area is a possibility, but not the only one, and it looks quite odd.

 

[jamie.j1989]

f the angle to the horizontal is θ, the probability of the angle being between θ and θ+dθ is sec²(θ)dθ.
If you want all angles equally likely, you need the probability to be (4/π)dθ.

I understand why the probability of the that the line goes through a point y+dy is dy as dy as a fraction of the entire length of the unit square is just dy/1=dy. But surely the probability of it going through the corresponding angle θ+dθ to go through a point on the x=1 vertical line is, from y=tanθ, cos²(θ)dy? Which would give more favourable oblique paths.

 

[haruspex]

I understand why the probability of the that the line goes through a point y+dy is dy as dy as a fraction of the entire length of the unit square is just dy/1=dy. But surely the probability of it going through the corresponding angle θ+dθ to go through a point on the x=1 vertical line is, from y=tanθ, cos²(θ)dy? Which would give more favourable oblique paths.

Consider dividing the (1,0) to (1,1) line into tengths of 0.1. With your scheme each of those has equal probability. Out towards the (1,1) end, the lines from the origin get bunched closer together, spreading the same 0.1 probability over progressively narrower ranges of angles. Thus the probability density of a given angle increases. sec increases, cos decreases.
Algebraically, y=tanθ, dy =sec²(θ)dθ. The probability that the line hits between y and y+dy is dy, so the probability that the angle is between θ=atan(y) and θ+dθ=atan(y+dy) is sec²(θ)dθ.

 

[jamie.j1989]

That is what you average, it is not what you average over.

As an example, consider a die which has faces "1", "1", "4", "4", "4", "4". What is the average? You can average over the result of many rolls: 3. But you can also average over the possible results (1 and 4): 2.5. This example might look a bit constructed, but you have exactly this problem with your cube: It is unclear how to weight the different possible results relative to each other. By surface area is a possibility, but not the only one, and it looks quite odd.

I think i understand, I want to average over all possible paths regardless of degeneracy. So is my approach possible or would a change of method by surface area be easier?

 

[jamie.j1989]

Consider dividing the (1,0) to (1,1) line into tengths of 0.1. With your scheme each of those has equal probability. Out towards the (1,1) end, the lines from the origin get bunched closer together, spreading the same 0.1 probability over progressively narrower ranges of angles. Thus the probability density of a given angle increases. sec increases, cos decreases.
Algebraically, y=tanθ, dy =sec²(θ)dθ. The probability that the line hits between y and y+dy is dy, so the probability that the angle is between θ=atan(y) and θ+dθ=atan(y+dy) is sec²(θ)dθ.

I don't see how that's the probability for a particular angle, it's equal to dy=sec²(θ)dθ which is the probability that the path goes through a point between y and dy, which also isn't constant as was first suggested?

 

[mfb]

For your box, you don't have degeneracy, you have a continuous problem. It is up to you to determine what you want to average over.

Where does the original problem come from?

 

[haruspex]

I don't see how that's the probability for a particular angle, it's equal to dy=sec²(θ)dθ which is the probability that the path goes through a point between y and dy, which also isn't constant as was first suggested?

Not sure what you are saying. Your initial approach was as though the probability of passing between y and y+dy was proportional to dy. If all directions are to be considered equally likely, you need it to be proportional to dθ. Clearly these are not the same.

 

[jamie.j1989]

For your box, you don't have degeneracy, you have a continuous problem. It is up to you to determine what you want to average over.

Where does the original problem come from?

I just want to average over all possible paths through the box, Its something I thought of and wanted to try and solve. So am I right in saying that my current method is only averaging over all possible paths from a fixed entry point? And I'm being biased with oblique angles as pointed out by haruspex due to using cartesian coordinates?

 

[mfb]

So am I right in saying that my current method is only averaging over all possible paths from a fixed entry point? And I'm being biased with oblique angles as pointed out by haruspex due to using cartesian coordinates?

Yes to both.