- #1
- 1,650
- 246
I read this problem in a "book" in my dreams  so I want to make sure the problem and my solution are not flawed.
so I want to make sure the problem and my solution are not flawed.
(I modified it a bit when I woke up; you know how dreams can be )
)
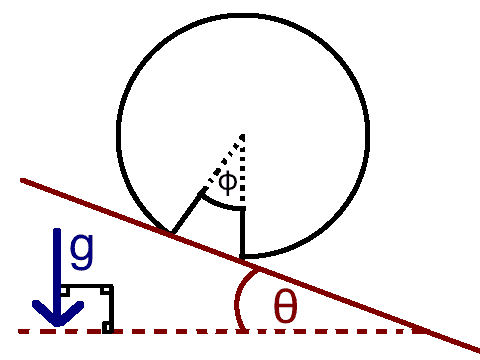
A cylinder of radius R has a section of angle Φ cut out as shown. After cutting this piece out, the mass is M.
The rotational inertia is then measured to be ##\beta MR^2##.
If the cylinder is now placed on an inclined plane of angle θ with the horizontal, then the center of mass may approach an average-terminal-speed.
(Averaged over a total cycle, i.e. when the cylinder turns 2pi*n radians about it's center; where n is an integer.)
Once this average-terminal-speed is obtained, find the maximum speed of the center of mass of the cylinder.
Assume the cylinder does not slip.
Assume the cylinder does not bounce.
Assume that after cutting the cylinder, the center of mass lies in the geometrical center of the uncut cylinder.
 2. General idea for the solution
2. General idea for the solution
kinetic energy lost in collision = kinetic energy gained in rolling down the plane
If the CoM speed is too large, more energy will be lost in the collision than is gained from gravity, and the cylinder will slow down.
Similarly, if the CoM speed is too small, it will gain more energy than it loses and speed up.
So the speed will always approach an average-terminal-speed. (Correct?)
Now let us assume this average-terminal-speed is obtained.
When the corner is just about to touch down (as shown in the image) the velocity of the center of mass (call it V0 at that point) will be greatest (which we want to find) and it will be in a direction Φ/2 below the (down-hill) direction of the plane (because it is rotating about the other corner). Since the cylinder doesn't bounce, all velocity perpendicular to the plane will be lost, leaving a final velocity of V0cos(Φ/2) after the collision.
The energy before the collision: ##0.5M(V_0^2+\beta R^2 \omega^2)=0.5MV_0^2(1+\beta)##
The energy after the collision: ##0.5MV_0^2\cos^2(\frac{\phi}{2})(1+\beta)##
The energy lost: ##0.5MV_0^2(1+\beta)\big(1-\cos^2(\frac{\phi}{2})\big)##By the time it gets back to the position in the picture, it will have traveled a distance 2πR down the plane, gaining a kinetic energy of 2πR*sin(θ)*MgEquating the previous two expressions we get: ##V_0 = \sqrt{ \frac{4\pi Rg\sin(\theta)}{(1+\beta)\big(1-\cos^2(\frac{\phi}{2})\big)} }##Is this a valid problem/solution?
(Anything I unconsciously assumed?)
 so I want to make sure the problem and my solution are not flawed.
so I want to make sure the problem and my solution are not flawed.(I modified it a bit when I woke up; you know how dreams can be
 )
)Homework Statement
A cylinder of radius R has a section of angle Φ cut out as shown. After cutting this piece out, the mass is M.
The rotational inertia is then measured to be ##\beta MR^2##.
If the cylinder is now placed on an inclined plane of angle θ with the horizontal, then the center of mass may approach an average-terminal-speed.
(Averaged over a total cycle, i.e. when the cylinder turns 2pi*n radians about it's center; where n is an integer.)
Once this average-terminal-speed is obtained, find the maximum speed of the center of mass of the cylinder.
Assume the cylinder does not slip.
Assume the cylinder does not bounce.
Assume that after cutting the cylinder, the center of mass lies in the geometrical center of the uncut cylinder.
kinetic energy lost in collision = kinetic energy gained in rolling down the plane
The Attempt at a Solution
If the CoM speed is too large, more energy will be lost in the collision than is gained from gravity, and the cylinder will slow down.
Similarly, if the CoM speed is too small, it will gain more energy than it loses and speed up.
So the speed will always approach an average-terminal-speed. (Correct?)
Now let us assume this average-terminal-speed is obtained.
When the corner is just about to touch down (as shown in the image) the velocity of the center of mass (call it V0 at that point) will be greatest (which we want to find) and it will be in a direction Φ/2 below the (down-hill) direction of the plane (because it is rotating about the other corner). Since the cylinder doesn't bounce, all velocity perpendicular to the plane will be lost, leaving a final velocity of V0cos(Φ/2) after the collision.
The energy before the collision: ##0.5M(V_0^2+\beta R^2 \omega^2)=0.5MV_0^2(1+\beta)##
The energy after the collision: ##0.5MV_0^2\cos^2(\frac{\phi}{2})(1+\beta)##
The energy lost: ##0.5MV_0^2(1+\beta)\big(1-\cos^2(\frac{\phi}{2})\big)##By the time it gets back to the position in the picture, it will have traveled a distance 2πR down the plane, gaining a kinetic energy of 2πR*sin(θ)*MgEquating the previous two expressions we get: ##V_0 = \sqrt{ \frac{4\pi Rg\sin(\theta)}{(1+\beta)\big(1-\cos^2(\frac{\phi}{2})\big)} }##Is this a valid problem/solution?
(Anything I unconsciously assumed?)
Last edited: