Average velocity, displacement vector.

[Shpat Celiku]

Homework Statement

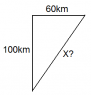
Suppose that a car moves up north 100 km for 2 h and then turns towards east
and travels in this direction 60 km for 1 h.
a. Draw in the following diagram the displacement vector of the car?
b. Determine the average velocity and the speed of the car.
c. Answer the question (b), if in the second part of the motion the driver would have
traveled the same distance (60 km) for the same time (1 h), but toward south.2. The attempt at a solution
a) No idea.
b) 100+60/2+1=53.3km/h
c) 100-60/2+1=13.3km/h

I'm not sure about any of them.

 

[mfb]

a) This is like a path on a map. Make north "up", south "down" and so on and choose a convenient scale, so you can draw the motion of the car in the graph.

b) 100+60/2+1=53.3km/h

I guess you mean (100km+60km)/(2h+1h). This is the average speed. It is not the average velocity.
What is the position of the car after those 3 hours? How far away from its initial position is it?

c) 100-60/2+1=13.3km/h

Why did you subtract the 60 here and added them at (b)? The car changed its direction in both cases.

 

[Shpat Celiku]

b) It's 160 km away from its initial position..How can i find the average velocity?

c) Cmon man if i knew how to do it i wouldn't be asking for help :/

 

[mfb]

b) It's 160 km away from its initial position..

It is not. Did you draw a sketch?

c) Cmon man if i knew how to do it i wouldn't be asking for help :/

I assume you did not blindly put together symbols, so why did you choose the calculations you posted?

 

[Shpat Celiku]

b)100 km north,then 60 km east...the displacement is from 0 to that point?

c) He traveled 100 km north and traveled another 60 back.

I don't know..i'm not very good at this as you can see.Now can you help me please?

 

[mfb]

b)100 km north,then 60 km east...the displacement is from 0 to that point?

Yes, but how far away is that point if you have a direct connection?

c) He traveled 100 km north and traveled another 60 back.

Okay. But he did not continue to travel 60 in (b).

Now can you help me please?

That's what I am doing here.

 

[Shpat Celiku]

He didn't?..It says he traveled 100 km north, changed direction and traveled another 60 km east.
Isn't average velocity formula : v : displacement/time ?

That's what I am doing here.

I know,i'm sorry.It's just that my deadline is tonight and I'm really stressed.

 

[mfb]

He didn't?..It says he traveled 100 km north, changed direction and traveled another 60 km east.

Sure, he made a detour. How far would the direct way be?

Isn't average velocity formula : v : displacement/time ?

Yes, and the displacement is the length of the direct way which I asked for.

 

[Shpat Celiku]

I still think it's 160 if it was a straight road :/...Can you explain why it's not and how to find the displacement?

 

[mfb]

I attached a sketch you should have already now. Do you really think X is as long as the other two sides together?

 

[Shpat Celiku]

X is 80.
so V=80/t...should t be 3 or t final - t initial which i think is 2 ?

 

[Shpat Celiku]

I think it's V=80km/3h=26.6 km/h

 

[mfb]

X shorter than the vertical line? No, certainly not.
Many mistakes can be found with cross-checks as simple as that.

What do you mean with t final and t initial? The car needed 3 hours to go from the original point to the final point.

 

[Shpat Celiku]

Well as you can see I'm not getting it.
Can you tell me the value of X?
And then show me how to solve c) because we are both getting tired.

 

[Shpat Celiku]

last try
is X 116.61?

 

[mfb]

Yes it is.

 

[Shpat Celiku]

And in c) is X 40?

 

[haruspex]

Yes

And in c) is X 40?

 

[Shpat Celiku]

Thank you very much:)