- #1
Master1022
- 611
- 117
- Homework Statement
- A design of an axial flow gas turbine stage is conducted for the following parameters at the mean radius:
Stage inlet stagnation conditions:
Flow angle at stator exit = 65 degrees
Stage reaction = 0.5
Flow coefficient =
Static pressure at stage exit:
Total-to-static efficiency:
Assuming the constant axial velocity across the stage, and air as working fluid (
i) the specific work done by the gas,
ii) the blade speed,
iii) the static temperature at the stage exit.
- Relevant Equations
- Euler work equation
Hi,
I was attempting the following turbo machinery problem and am getting quite stuck on the first part of the question. The question is:
A design of an axial flow gas turbine stage is conducted for the following parameters at the mean radius:
Stage inlet stagnation conditions:
Flow angle at stator exit = 65 degrees
Stage reaction = 0.5
Flow coefficient =
Static pressure at stage exit:
Total-to-static efficiency:
Assuming the constant axial velocity across the stage, and air as working fluid (
i) the specific work done by the gas,
ii) the blade speed,
iii) the static temperature at the stage exit.
Attempt:
(i) the specific work done by the gas
I am not sure how to make progress in this area. From looking at the data given in the question, I am trying to extract the useful information and draw the following velocity triangles:
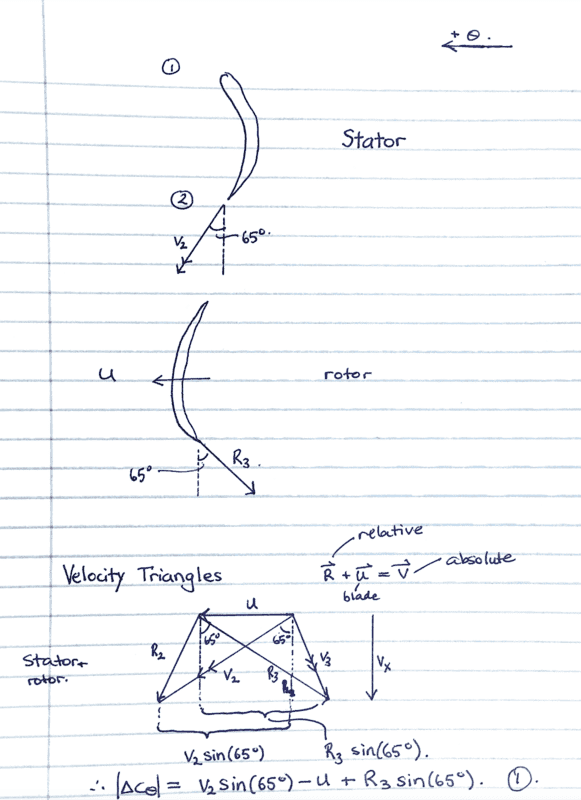
From there, we are told that the axial velocity is constant across the stage and can thus write:
Substituting this into equation (1) from the picture (bottom of page), which is the magnitude of the change of the whirl velocity then turns it into:
Thus from the Euler work equation:
However, I think this will only be useful for the second part of the question...
Returning back to trying to find the work, I was thinking that perhaps I could go down the route of:
1. Use relation between stagnation enthalpy and stagnation pressure to get
2. Using SFEE to relate specific work and change in stagnation enthalpy
So this method would start with the thermodynamic relation:
However, this makes the assumption that the density is constant which perhaps isn't correct to assume... Then we could assume that the stagnation pressure across the stator such that
I am not really sure if I am missing out a formula or concept that would help me here. Any guidance would be really appreciated.
I was attempting the following turbo machinery problem and am getting quite stuck on the first part of the question. The question is:
A design of an axial flow gas turbine stage is conducted for the following parameters at the mean radius:
Stage inlet stagnation conditions:
Flow angle at stator exit = 65 degrees
Stage reaction = 0.5
Flow coefficient =
Static pressure at stage exit:
Total-to-static efficiency:
Assuming the constant axial velocity across the stage, and air as working fluid (
i) the specific work done by the gas,
ii) the blade speed,
iii) the static temperature at the stage exit.
Attempt:
(i) the specific work done by the gas
I am not sure how to make progress in this area. From looking at the data given in the question, I am trying to extract the useful information and draw the following velocity triangles:
From there, we are told that the axial velocity is constant across the stage and can thus write:
Substituting this into equation (1) from the picture (bottom of page), which is the magnitude of the change of the whirl velocity then turns it into:
Thus from the Euler work equation:
However, I think this will only be useful for the second part of the question...
Returning back to trying to find the work, I was thinking that perhaps I could go down the route of:
1. Use relation between stagnation enthalpy and stagnation pressure to get
2. Using SFEE to relate specific work and change in stagnation enthalpy
So this method would start with the thermodynamic relation:
However, this makes the assumption that the density is constant which perhaps isn't correct to assume... Then we could assume that the stagnation pressure across the stator such that
I am not really sure if I am missing out a formula or concept that would help me here. Any guidance would be really appreciated.