karush
Gold Member
MHB
- 3,240
- 5
$\textit{given $y''+y'-2y=0\quad y(0)=1 \quad y'(0)=1$ }$
\begin{align*}\displaystyle
\textit{if } r&=e^{t} \textit{then:}\\
y''+y'-2y&=r^2+r-2=(r+2)(r-1)=0\\
&=c_1^{2t}+c_2^{-t}\\
y&=\color{red} {e^t; \quad y \to \infty \,as \, t \to \infty }
\end{align*}ok the bk answer is in red
I just don't get this
why do we need $$y(0)=1 \quad y'(0)=1$$
the graph of $y=e^t$
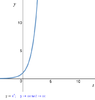
\begin{align*}\displaystyle
\textit{if } r&=e^{t} \textit{then:}\\
y''+y'-2y&=r^2+r-2=(r+2)(r-1)=0\\
&=c_1^{2t}+c_2^{-t}\\
y&=\color{red} {e^t; \quad y \to \infty \,as \, t \to \infty }
\end{align*}ok the bk answer is in red
I just don't get this
why do we need $$y(0)=1 \quad y'(0)=1$$
the graph of $y=e^t$

Last edited: