B-field for a half-infinitely long wire

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

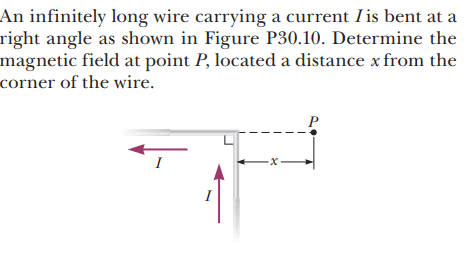
The solution is

However, I would like to understand how to solve this using Biot–Savart Law.

So far my working is:

$\vec {dB} = \frac {\mu_0Ids\sin\theta} {4\pi r^2}$

However, I'm not sure what to do about the $r^2$ since the wire is infinitely long. I am thinking about having the limits of integration to be $\theta_1 = 0$ and $\theta_2 = \frac {\pi} {2}$

Many thanks!

 

[haruspex]

.So far my working is:

$\vec {dB} = \frac {\mu_0Ids\sin\theta} {4\pi r^2}$

Knowing a formula is of no value unless you know what all the variables mean and in what context the formula applies.
Please state what those variables mean here. From that you should be able to answer your question.

 

[anuttarasammyak]

As your LHS is vector, RHS should be vector also. Check it out.

 

[member 731016]

Knowing a formula is of no value unless you know what all the variables mean and in what context the formula applies.
Please state what those variables mean here. From that you should be able to answer your question.

Thank you for your reply @haruspex!

$\mu_0$ is the magnetic permeability of free space
$I$ is the current in the vertical wire
$ds$ is the length element of the wire
$r^2$ is the distance from each $ds$ to point $P$

I think the thing that was tripping me up was that I thinking that we could call the infinite length to be $a$ which would mean that $\tan\theta = \frac {x} {a}$ however this would be zero since $a \rightarrow \infty$ then $\tan \theta \rightarrow 0$. I was then going to solve for $\theta$ and have limits of integration to be angles $\theta_1 = 0$ and $\theta_2 = \frac {\pi} {2}$. However now I think I should get $r$ in terms of $\sin\theta$. I will try to solve that now. Is my reasoning correct so far?

 

[member 731016]

As your LHS is vector, RHS should be vector also. Check it out.

Thanks @anuttarasammyak ! Sorry both sides should have $-\hat k$ as the direction.

 

[haruspex]

I should get $r$ in terms of $\sin\theta$.

Yes.

 

[Alex Schaller]

 

[member 731016]

Yes.

Thank you @haruspex !

 

[member 731016]

View attachment 321223
View attachment 321224
View attachment 321225

Thank you for your solution @Alex Schaller! :)

 

[Alex Schaller]

Thank you for your solution @Alex Schaller! :)

You are welcome