Trikenstein
- 21
- 9
- TL;DR Summary
- An object located at the equator is free falling. Does it fall straight with or without radial deviation?
We have a weekly fun random chat to break from the routine of WFH. A science quiz poped up. There is no consensus on the good answer. We need 3rd party opinion.
You are at the equator, dropping a steel ball into a dry well, the depth is 100 meters, the mass of the ball is 1kg. The starting point is the top center of the well. Where will the ball land at the bottom? Only the position of the contact point is asked. What happened after contact is not needed.
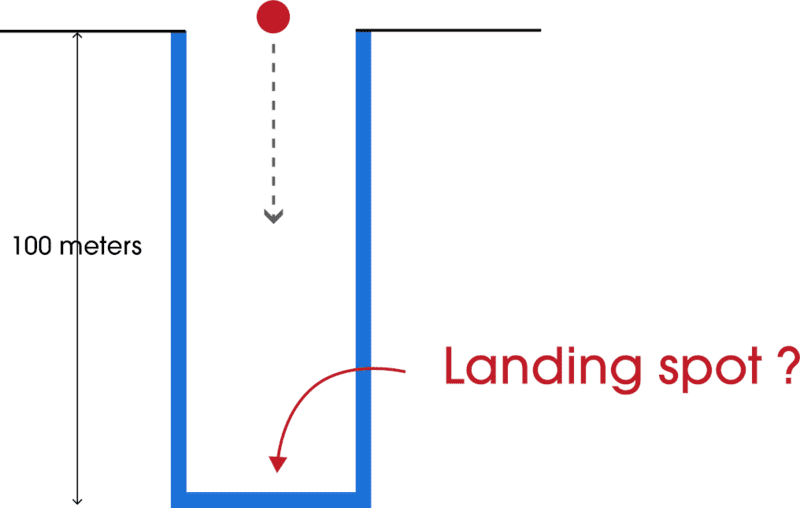
The initial conditions are ideal:
Air resistance/turbulence is ignored
The ball is a perfect sphere, released from the top center, zero spin, zero initial speed.
The well is a perfect cylinder, and perfectly vertical.
Environmental factors ignored (rain, wind, etc...)
There is no trick, no trap, no joke in the question. You are allowed to get additional data to support your answer. As long as it is compatible with known physical laws. For example, if you need the value of Earth gravity, please look it up.
There is no need to give an answer accurate to the nanometer. Only the reasoning is important. For example, micro-gravity variation could be ignored.
So far we have gathered several answers, which boil down to this:
You are at the equator, dropping a steel ball into a dry well, the depth is 100 meters, the mass of the ball is 1kg. The starting point is the top center of the well. Where will the ball land at the bottom? Only the position of the contact point is asked. What happened after contact is not needed.
The initial conditions are ideal:
Air resistance/turbulence is ignored
The ball is a perfect sphere, released from the top center, zero spin, zero initial speed.
The well is a perfect cylinder, and perfectly vertical.
Environmental factors ignored (rain, wind, etc...)
There is no trick, no trap, no joke in the question. You are allowed to get additional data to support your answer. As long as it is compatible with known physical laws. For example, if you need the value of Earth gravity, please look it up.
There is no need to give an answer accurate to the nanometer. Only the reasoning is important. For example, micro-gravity variation could be ignored.
So far we have gathered several answers, which boil down to this:
- ANSWER1: landing spot is dead center at the bottom. The reasoning is because there is no external force influencing the sideway motion of the ball, therefore it drops straight down, with zero deviation from the center.
- ANSWER2: off-center, 32 millimeters toward the East. The submitter justifies by a half page of calculation. Please allow me to hold back temporarily the publishing of the details of this answer. Actually I am curious to know what other people would come up with if they have no prior knowledge of this answer.
Last edited: