EE18
- 112
- 13
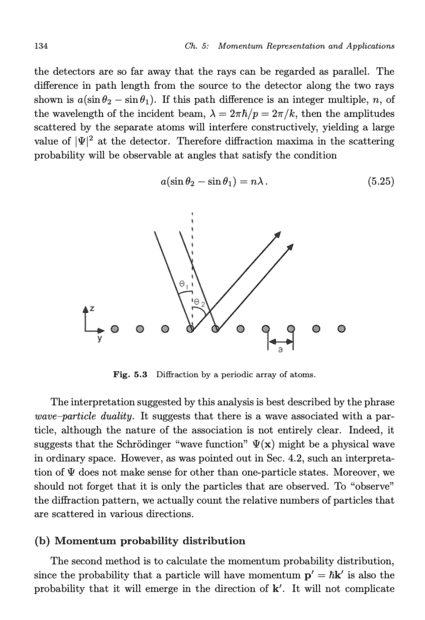
In Chapter 5.4b of Ballentine, a discussion ensues about the analysis of a particle scattering off of a (Bravais lattice) periodic array. I attach pictures here of the full discussion in case anyone wants/needs to refer to it, but I am particularly baffled by the discussion on page 135. In particular, my understanding is as follows:
(1) As a general goal, we are looking for an eigenstate (i.e. solution to (5.24) -- what Ballentine often refers to as a "physical solution") which respects the boundary condition that it is incident from some source which we capture vaguely based on the ultimate ##e^{i\textbf{k} \cdot \textbf{x}}## in (5.27) which is to be discussed.
(2) We employ Bloch's Theorem which tells us that it is possible to pick an eigenbasis of the Hamiltonian (i.e. of (5.24)) in which every solution is of the form (5.26). That it is possible is important -- it does not, in particular, follow that every eigenstate obeying (5.24) is of the form (5.26).
(3) My issue is with why Ballentine says, at the bottom of 135, that (5.27) must be of the form (5.26). Why!? I'm satisfied with the paragraph above (5.27) where we argue that we need only one eigenstate of the form (5.26) to account for the first term in (5.27), but why should we in general say that that one eigenstate (for the given ##\textbf{q}=\textbf{k}_{xy}## is then sufficient to account for all the other terms in (5.27)? That doesn't seem to have been established at all, and I could imagine that there would be other ##\textbf{q}## in the eigenspace of ##H## corresponding to the given value of ##E## so that, from my comments in (2), we in general have to bring in other eigenstates of the form (5.26) to write (5.27)? Ballentine must be using some other information to exclude this possibility.



(1) As a general goal, we are looking for an eigenstate (i.e. solution to (5.24) -- what Ballentine often refers to as a "physical solution") which respects the boundary condition that it is incident from some source which we capture vaguely based on the ultimate ##e^{i\textbf{k} \cdot \textbf{x}}## in (5.27) which is to be discussed.
(2) We employ Bloch's Theorem which tells us that it is possible to pick an eigenbasis of the Hamiltonian (i.e. of (5.24)) in which every solution is of the form (5.26). That it is possible is important -- it does not, in particular, follow that every eigenstate obeying (5.24) is of the form (5.26).
(3) My issue is with why Ballentine says, at the bottom of 135, that (5.27) must be of the form (5.26). Why!? I'm satisfied with the paragraph above (5.27) where we argue that we need only one eigenstate of the form (5.26) to account for the first term in (5.27), but why should we in general say that that one eigenstate (for the given ##\textbf{q}=\textbf{k}_{xy}## is then sufficient to account for all the other terms in (5.27)? That doesn't seem to have been established at all, and I could imagine that there would be other ##\textbf{q}## in the eigenspace of ##H## corresponding to the given value of ##E## so that, from my comments in (2), we in general have to bring in other eigenstates of the form (5.26) to write (5.27)? Ballentine must be using some other information to exclude this possibility.