- #1
anniecvc
- 28
- 0
I know to find the angle between two vectors you would take the arccosine of the dot product of the two vectors divided by the magnitude of both vectors multiplied.
I know the angle between two vectors is always less than or equal to 180 degrees.
The angle can only be found when both vectors begin at the same origin and point outward, or when both vectors begin a different origins but end at the same point:
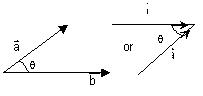
Why can't we find the angle between two vectors where one points out and the other terminates at the former's origin? What is the significance of both beginning at the same origin or both terminating at the same endpoint?
I know the angle between two vectors is always less than or equal to 180 degrees.
The angle can only be found when both vectors begin at the same origin and point outward, or when both vectors begin a different origins but end at the same point:
Why can't we find the angle between two vectors where one points out and the other terminates at the former's origin? What is the significance of both beginning at the same origin or both terminating at the same endpoint?