tellmesomething
- 443
- 68
- Homework Statement
- Can there be a negative infinitesmal?
- Relevant Equations
- None
What I mean is on a coordinate plane like below we take the positive x axis measure a certain distance x on it and take the infinitesmally small quantity dx next to it in the positive direction:
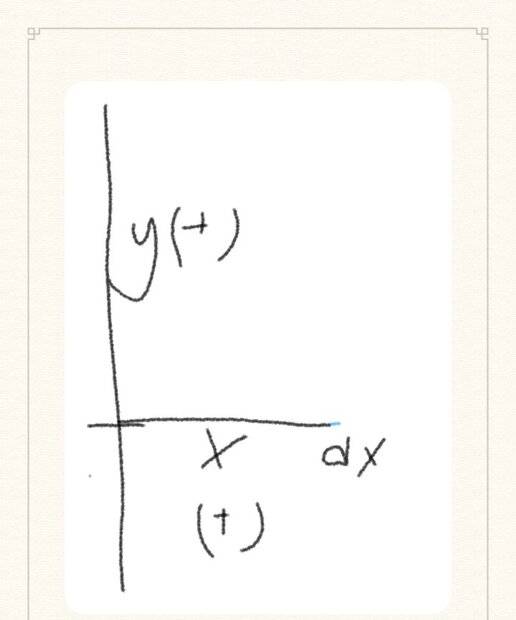
Now can I do the opposite as in can I measure a distance negative x on the negative x axis and take an infinitesmal quantity?:
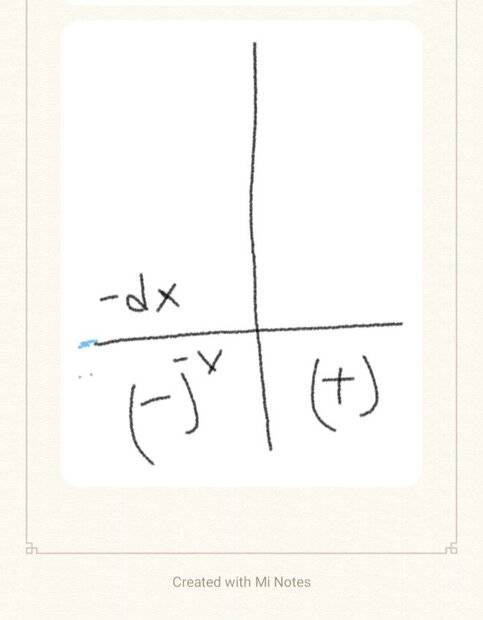
Now can I do the opposite as in can I measure a distance negative x on the negative x axis and take an infinitesmal quantity?: