Undergrad Basic standard deviation calculation

Click For Summary
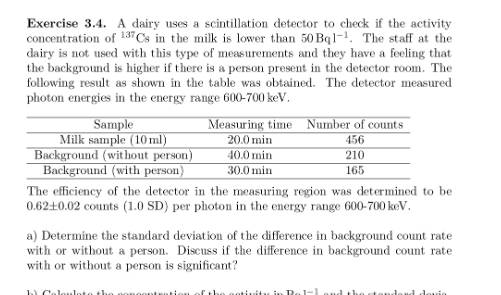
The discussion focuses on the calculation of standard deviation (SD) and its relationship with rate and time. It clarifies that the standard deviation of total counts (n) is expressed as √n, while the rate (r) is defined as n/t. The equations presented demonstrate how changes in counts (Δn) and rate (Δr) relate to time. The conversation highlights the importance of squaring in the denominator for accurate calculations. Overall, the thread emphasizes understanding the foundational equations for standard deviation in relation to counts and rates.
Graham87
Messages
72
Reaction score
16
I don’t get how they got the equation for the standard deviation. Why do they only square with the time in the denominator?

Thanks!

4A5AE19B-D40A-40F4-BA74-4ADD1416F63E.jpeg

A536CA42-AB1E-4112-ABF7-E055104CC803.jpeg
 
Physics news on Phys.org
We know that the SD of the total number of counts n is √n and rate r =n/t

So;
n=rt
Δn = (Δr)⋅t =√(n/t)t
Δr=√(n)/t =√(n/t2)
 
gleem said:
We know that the SD of the total number of counts n is √n and rate r =n/t

So;
n=rt
Δn = (Δr)⋅t =√(n/t)t
Δr=√(n)/t =√(n/t2)
Aha! Thanks!
 

Thread 'How do E[X] and E[|X|] relate?'

Greetings, I am studying probability theory [non-measure theory] from a textbook. I stumbled to the topic stating that Cauchy Distribution has no moments. It was not proved, and I tried working it via direct calculation of the improper integral of E[X^n] for the case n=1. Anyhow, I wanted to generalize this without success. I stumbled upon this thread here: https://www.physicsforums.com/threads/how-to-prove-the-cauchy-distribution-has-no-moments.992416/ I really enjoyed the proof...
View full post »

Similar threads

High School Variance & Standard Deviation
  • · Replies 42 ·
2
Replies
42
Views
5K
Undergrad Error bars in Excel (standard deviation, standard error, percentage)
  • · Replies 4 ·
Replies
4
Views
3K
Undergrad Confidence interval on Standard deviation
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Correctly Scaling the Standard Deviation for Scaled Measurements
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad The Standard Deviation of Sample vs. Population in Probability Calculations
  • · Replies 18 ·
Replies
18
Views
3K
Undergrad Standard deviation question -- population std vs sample std
  • · Replies 5 ·
Replies
5
Views
3K
High School Standard Deviation as Function of Sample Size
  • · Replies 24 ·
Replies
24
Views
6K
Undergrad Standard Deviation Versus Sample Size & T-Distribution
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Using standard deviation values as independent variables
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Standard Deviation from one axis to another axis
  • · Replies 4 ·
Replies
4
Views
3K