Basics of forces/torques and fulcrum

[JohnnyLaws]

TL;DR Summary: When a cube is supported at the fulcrum and remains stationary due to a balloon exerting a force in the opposite direction of its weight.

So the exercise is as follows: We have a homogeneous cube with an edge length of 2 meters, weighing 98N. On the other hand, we have a balloon that is applying an upward force with a magnitude of 78.4N. What is the distance at which I need to place the balloon for the cube to remain static?

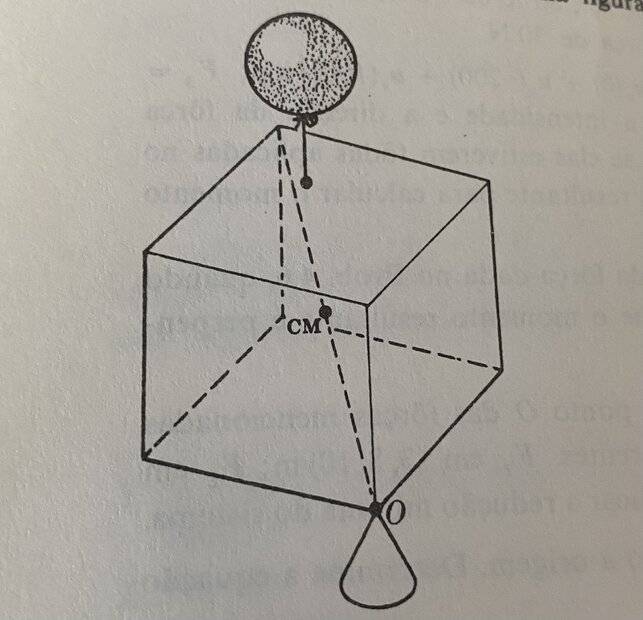
I think to solve this exercise, I need to add up all the torques and set the equation to 0, but I can't get anywhere with this. The solution to that exercise states that the balloon needs to be placed at a distance of 1.77 meters from the fulcrum and, at the same time, aligned with the cube's diagonals.

 

[Doc Al]

I think to solve this exercise, I need to add up all the torques and set the equation to 0, but I can't get anywhere with this.

Sounds good to me. What have you done so far? (Hint: Measure distances from the corner of the cube.)

 

[Doc Al]

The solution to that exercise states that the balloon needs to be placed at a distance of 1.77 meters from the fulcrum and, at the same time, aligned with the cube's diagonals.

I wouldn't call that answer the "distance from the fulcrum" since the fulcrum is at the bottom of the cube. But if you measure distances along the top of the cube from the corner directly above the fulcrum, you'll get the given answer.

 

[Lnewqban]

...I think to solve this exercise, I need to add up all the torques and set the equation to 0, but I can't get anywhere with this.

Welcome, @JohnnyLaws !

Could you show us how far did you get?
Do you know how to draw a free body diagram?

 

[JohnnyLaws]

Welcome, @JohnnyLaws !

Could you show us how far did you get?
Do you know how to draw a free body diagram?

I think I do. Basically I drew a cube after that I put the force of weight in center of mass, the force of the ballon above cube and a force in fulcrum pointing up.
I think what I'm doing wrong is the cross product because in the equation of torques the unic variable is the position and position have 3 different components and I don't know any of them

 

[jbriggs444]

I think I do. Basically I drew a cube after that I put the force of weight in center of mass, the force of the ballon above cube and a force in fulcrum pointing up.

Yes. Those are the three forces.

Have you decided on a reference axis yet for computing the torques from those forces? If you choose a reference axis at the right place, you can eliminate one of those forces from the torque balance.

I think what I'm doing wrong is the cross product because in the equation of torques the unic variable is the position and position have 3 different components and I don't know any of them

Have you picked your coordinate axes yet? Since all three forces are vertical, you can align one of your axes that way and ignore that coordinate.

Since there is symmetry, you can align one of your axes that way and eliminate a second coordinate.

Now you have a one dimensional problem involving two forces.

 

[Lnewqban]

I think I do. Basically I drew a cube after that I put the force of weight in center of mass, the force of the ballon above cube and a force in fulcrum pointing up.
I think what I'm doing wrong is the cross product because in the equation of torques the unic variable is the position and position have 3 different components and I don't know any of them

Please, see:
https://www.physicsclassroom.com/class/newtlaws/Lesson-2/Drawing-Free-Body-Diagrams

Having a cube tells you the spatial location of its center of mass (and its vertical weight force) respect to the pivot point (and its vertical reaction force) and the vertical force exerted by the balloon.