Bead on a rotating stick and the Lagrangian

[LCSphysicist]

Homework Statement

A stick is pivoted at the origin and is arranged to swing around in a
horizontal plane at constant angular speed ω. A bead of mass m slides
frictionlessly along the stick. Let r be the radial position of the bead.
Find the conserved quantity E given in Eq. (6.52). Explain why this
quantity is not the energy of the bead.

Relevant Equations

All below...

A stick is pivoted at the origin and is arranged to swing around in a
horizontal plane at constant angular speed ω. A bead of mass m slides
frictionlessly along the stick. Let r be the radial position of the bead.
Find the conserved quantity E given in Eq. (6.52). Explain why this
quantity is not the energy of the bead.

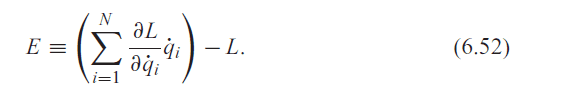
I came across with such question and i am a little confuse with the answer.
$$L = \frac{m(r'^{2} + (r\theta ')^{2})}{2}$$
$$E = \frac{m(r'^{2} + (r\theta ')^{2})}{1}- \frac{m(r'^{2} + (r\theta ')^{2})}{2}$$
$$E = \frac{m(r'^{2} + (r\theta ')^{2})}{2}$$

But the answer should be... $$E = \frac{m(r'^{2} - (r\theta ')^{2})}{2}$$

 

[etotheipi]

Since $\dot{\theta} = \omega$ is constant, $L = L(r)$ only. So $\frac{\partial L}{\partial \dot{r}} \dot{r} = m\dot{r}^2$ but $\frac{\partial L}{\partial \dot{\theta}} = 0$. Then, since $L = T - V = T = \frac{1}{2} m \dot{r}^2 + \frac{1}{2}mr^2 \omega^2$, you get the desired result, i.e. the conserved quantity is$$Q = \frac{1}{2}m\dot{r}^2 - \frac{1}{2}mr^2 \omega^2$$but this is not the energy.

 

[LCSphysicist]

Since $\dot{\theta} = \omega$ is constant, $L = L(r)$ only. So $\frac{\partial L}{\partial \dot{r}} \dot{r} = m\dot{r}^2$ but $\frac{\partial L}{\partial \dot{\theta}} = 0$. Then, since $L = T - V = T = \frac{1}{2} m \dot{r}^2 + \frac{1}{2}mr^2 \omega^2$, you get the desired result, i.e. the conserved quantity is$$Q = \frac{1}{2}m\dot{r}^2 - \frac{1}{2}mr^2 \omega^2$$but this is not the energy.

Oh, My partial derivative with respect to the theta dot was wrong. Thx