Egghead44
- 6
- 4
- TL;DR Summary
- Beginner Question Regarding Entanglement
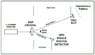
I am just starting to learn quantum mechanics. And have some questions on entanglement. I have learned that when there is two particles entangled that they share the same wave function and cannot be considered by themselves. I am having a hard time understanding some of the nuances of this concept. I have attached a diagram of the setup I have imagined. The setup uses a laser of 405nm to send photons thru a KDP crystal. This will produce two 810nm entangled photons, both having same polarity. This is then sent down two different paths, one photon (photon a) toward a 2 slit plate and the other (photon b), at half the distance, to a photon detector.
What will happen if you send one photon at a time through this setup in one of two different modes. In the first mode the APD detector is not used (taken out), and the second mode the APD detector is used. In the 1st mode, I imagine the 2 slit photons (photons a) will make a diffraction pattern. My question is in the 2nd mode, the one with the detector in place, will the photons going thru the 2 slit plate and sill interfere with each other? I am assuming that the collapse of photon B's wave function would collapse the photon A's wave function too. Or is this a wrong assumption?
What will happen if you send one photon at a time through this setup in one of two different modes. In the first mode the APD detector is not used (taken out), and the second mode the APD detector is used. In the 1st mode, I imagine the 2 slit photons (photons a) will make a diffraction pattern. My question is in the 2nd mode, the one with the detector in place, will the photons going thru the 2 slit plate and sill interfere with each other? I am assuming that the collapse of photon B's wave function would collapse the photon A's wave function too. Or is this a wrong assumption?