Bell's spaceship paradox

[Renato Iraldi]

TL;DR Summary

A popular explanation of the Bell's paradox

They concluded:
"One may conclude that whenever a body is constrained to move in such a way that all parts of it have the same acceleration with respect to an inertial frame (or, alternatively, in such a way that with respect to an inertial frame its dimensions are fixed, and there is no rotation), then such a body must in general experience relativistic stresses."
Popular Explanation
If we have an elastic band in our hands and we move the band and hands to the right, we will see that the distance between the hands and the band contracts. If we want to keep the distance between the hands always at the same distanceis constrained to move in such a way that all parts of it have the same acceleration with respect to an inertial frame , then we have to open them by stretching, also, the elastic band.


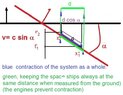
1 Epstein diagram. They are explained in the video

 

[haushofer]

I'm not sure whether this topic is a question, a general remark or a video promotion. Let me take my crystal ball to see.

 

[Dale]

I don't like Epstein diagrams. They are a thing, but I don't think that they are a good thing.

 

[Ibix]

I find the explanation in the text confusing because it misses out key points, like that the band must remain unstressed (or with the same stress in its final rest frame as it had in its initial rest frame) if it is to be seen to length contract. It's also not clear about what's being measured in which frame.

 

[Renato Iraldi]

I'm not sure whether this topic is a question, a general remark or a video promotion. Let me take my crystal ball to see.

I'm not sure whether this topic is a question, a general remark or a video promotion. Let me take my crystal ball to see.

crystal ball say: is a general remark, an example how a length contraction can stress an object.
I am trying to explain the paradox with Epstein's diagrams and I have not been able to include figures, that is why I have included a video explaining Epstein's interpretation that allows a better understanding of relativity and its paradoxes. Thank you for your comment

 

[Renato Iraldi]

I don't like Epstein diagrams. They are a thing, but I don't think that they are a good thing.

You don't like Epstein's diagrams because you haven't studied them, but I'm sure that if you study them you will appreciate them a lot. You will see a physical model that with some elementary instructions could construct the Lorentz transformations, and also all the strangenesses of relativity are understood geometrically (Euclidean geometry).
I am at your disposal to discuss with you. Riraldi@gmail.com

I find the explanation in the text confusing because it misses out key points, like that the band must remain unstressed (or with the same stress in its final rest frame as it had in its initial rest frame) if it is to be seen to length contract. It's also not clear about what's being measured in which frame.

I will give you a simple explanation, the two rockets leave linked by a rope with equal acceleration, after a certain time the pilots see the rope and there is no reason to see it broken.

Bell says if they have the same acceleration from the ground, they will always be seen at the same distance, but from the ground they should be observed contracted, therefore the motors have supplied the contraction, but the rope does not have motors and if it should look contracted, shorter than the distance between the planes. Then it must have broken.
I will discuss the paradox on my YouTube channel give me a week

 

[PeroK]

It's clear that if two rockets accelerate simultaneously from rest in an initial reference frame, then (by the relativity of simultaneity) they cannot accelerate simultaneously in any other frame (relative to the direction of the acceleration). In particular, in the instantaneous rest frame of one of the rockets, the acceleration of the other rocket must be out of sync.

No further explanation is needed. The paradox stems from using the term "equal" acceleration (i.e. "simultaneous" acceleration) and implicitly assuming that applies in all reference frames. There's no paradox at all - only the relativitity of simultaneity in a new guise.

 

[Ibix]

an example how a length contraction can stress an object.

I think one of the key points is that it is the rocket motors that stress the object, not the length contraction. Indeed, in the rope frame it is not contracted. What it has is a time varying stress, anf it is this that eventually causes the break.

You don't like Epstein's diagrams because you haven't studied them,

That's... quite an assumption. It's possible to understand something and not find it useful. I've yet to see a situation that, in my opinion, was better explained with an Epstein diagram than a Minkowski diagram.

I will give you a simple explanation,

I understand both how the question misleads you into a paradox and the mistake that you make to get yourself there. My criticism is that you aren't being clear about who is measuring the quantities you talk about. You also haven't stated the actual paradox (that the rope "should" go slack in the rope frame) nor the resolution, which is unequal acceleration of the rockets in the rope frame. At least, not in the text. I haven't watched the video yet.

 

[Renato Iraldi]

It's clear that if two rockets accelerate simultaneously from rest in an initial reference frame, then (by the relativity of simultaneity) they cannot accelerate simultaneously in any other frame (relative to the direction of the acceleration). In particular, in the instantaneous rest frame of one of the rockets, the acceleration of the other rocket must be out of sync.

No further explanation is needed. The paradox stems from using the term "equal" acceleration (i.e. "simultaneous" acceleration) and implicitly assuming that applies in all reference frames. There's no paradox at all - only the relativitity of simultaneity in a new guise.

It's clear that if two rockets accelerate simultaneously from rest in an initial reference frame, then (by the relativity of simultaneity) they cannot accelerate simultaneously in any other frame (relative to the direction of the acceleration). In particular, in the instantaneous rest frame of one of the rockets, the acceleration of the other rocket must be out of sync.

No further explanation is needed. The paradox stems from using the term "equal" acceleration (i.e. "simultaneous" acceleration) and implicitly assuming that applies in all reference frames. There's no paradox at all - only the relativitity of simultaneity in a new guise.

You are right if it accelerates equally and simultaneously in the ground system, it does not mean that it accelerates equally and simultaneously seen from the pilots' system. But if it is accelerated simultaneously from the ground system one can say that the distance between the planes always remains the same as seen from the ground but the rope does not, it contracts compared to the ground. therefore it breaks.

 

[PeroK]

But if it is accelerated simultaneously from the ground system one can say that the distance between the planes always remains the same as seen from the ground but the rope does not, it contracts compared to the ground. therefore it breaks.

The distance between the ends of the rope remains the same in the ground frame. But, in that frame the rope is moving, so we need to apply (the relativistic version of) Hooke's Law: the moving rope is under tension. You're trying to apply classical thinking to a rope in a relativistic scenario. Implicitly applying the non-relativistic Hooke's law. The rope is no longer at its relaxed length (in its own rest frame).

There's a good quotation in the book SR by Helliwell that if spacetime is not Newtonian, then we need to revisit all the physics that was derived using Newtonian space and time. We cannot assume that all the non-relativistic formulas for energy, momentum, angular momentum and the motion of springs or ropes remain unchanged.

 

[Dale]

You don't like Epstein's diagrams because you haven't studied them, but I'm sure that if you study them you will appreciate them a lot

If I had not studied them then I would have no opinion on them. I have studied them and as a result of studying them found that they are not good.

They can accomplish only one thing correctly. Given exactly two inertial frames you can use Epstein diagrams to graphically represent time dilation and length contraction. That is the only task that they are suited for. They fail at pretty much anything else.

You cannot analyze three frames this way. Suppose that you have frames A, B, and C. Draw the three lines such that $v_{AB}=\sin(\angle_{AB})$ and $v_{BC}=\sin(\angle_{BC})$, then you will find that $v_{AC}\ne\sin(\angle_{AC})$.

Similarly, even with two observers you cannot represent any exchange of light signals. A beam of light will be 90 degrees from an observers time axis, and will therefore not be 90 degrees from any other observer’s.

Intersections on Epstein diagrams do not imply collision/meeting, and a lack of an intersection on an Epstein diagram similarly does not imply a lack of a collision/meeting.

Points in Epstein diagrams have no physical meaning. No more than one pair of lines may have a physically meaningful angle in an Epstein diagram.

My decidedly negative opinion on Epstein diagrams is not based on ignorance. It is based on decades of experience with relativity, interest in pedagogy, and a study of alternative approaches including Epstein diagrams.

In my expert opinion, for learning relativity, Epstein diagrams are not good. Next time you disagree with my opinion, kindly ask me to justify it or ask me if I have studied it. Do not ignorantly assume that my opinion is based on ignorance.

 

[PeroK]

To make this clear, imagine a spring of natural length $L$. Now, without touching this spring, imagine it in a reference frame moving at some relativistic speed relative to the spring. The measured length of the spring in this reference frame is $L/\gamma$. So, this must be the natural length of the spring in that reference frame.

This tells us simply, without reference to spaceships or acceleration, that we must take account of the relative inertial motion of a spring when considering its natural length. And, it makes no sense to try to ignore this - through some sleight of hand or specious phraseology that produces a seemingly paradoxical scenario. If the spring is not subject to a stretching force, then it is shorter in a frame where it is moving. And, if it must remain its original, proper length in some frame where it is moving, then it must be subject to a stretching force.

All forces and motion are considered in the direction along the length of the spring.

 

[Renato Iraldi]

If I had not studied them then I would have no opinion on them. I have studied them and as a result of studying them found that they are not good.

They can accomplish only one thing correctly. Given exactly two inertial frames you can use Epstein diagrams to graphically represent time dilation and length contraction. That is the only task that they are suited for. They fail at pretty much anything else.

You cannot analyze three frames this way. Suppose that you have frames A, B, and C. Draw the three lines such that $v_{AB}=\sin(\angle_{AB})$ and $v_{BC}=\sin(\angle_{BC})$, then you will find that $v_{AC}\ne\sin(\angle_{AC})$.

Similarly, even with two observers you cannot represent any exchange of light signals. A beam of light will be 90 degrees from an observers time axis, and will therefore not be 90 degrees from any other observer’s.

Intersections on Epstein diagrams do not imply collision/meeting, and a lack of an intersection on an Epstein diagram similarly does not imply a lack of a collision/meeting.

Points in Epstein diagrams have no physical meaning. No more than one pair of lines may have a physically meaningful angle in an Epstein diagram.

My decidedly negative opinion on Epstein diagrams is not based on ignorance. It is based on decades of experience with relativity, interest in pedagogy, and a study of alternative approaches including Epstein diagrams.

In my expert opinion, for learning relativity, Epstein diagrams are not good. Next time you disagree with my opinion, kindly ask me to justify it or ask me if I have studied it. Do not ignorantly assume that my opinion is based on ignorance.

 

[Renato Iraldi]

I apologize, I am 82 years old and I had not seen Epstein's diagrams until recently, and people tend to think that ignorance itself can be shared.I see that you have more knowledge than I about Epstein's diagrams. especially regarding applications beyond the surface.I have reformed Epstein's theory (and I have managed to elaborate the Lorentz transformations in an elementary way and I am very enthusiastic.If you allow me, I will send you two diagrams by Epstein that illustrate Bell's paradox. At first the acceleration (increase in speed) shows us how the times measured by the pilots are not equal and are calculated with simple trigonometry.In the second, where the planes maintain their distance on the ground, you can clearly see how the rope breaks.It seems very illustrative to me.Apologies again and thank you for your interest.Renato

 

[PeterDonis]

how a length contraction can stress an object

"Length contraction" is frame dependent, and frame dependent quantities have no physical meaning. Actual physics is done with invariants, things that don't depend on which frame you choose.

The invariant that explains why the string in the Bell's spaceship paradox scenario gets stressed is the expansion scalar being positive.

 

[Renato Iraldi]

The distance between the ends of the rope remains the same in the ground frame. But, in that frame the rope is moving, so we need to apply (the relativistic version of) Hooke's Law: the moving rope is under tension. You're trying to apply classical thinking to a rope in a relativistic scenario. Implicitly applying the non-relativistic Hooke's law. The rope is no longer at its relaxed length (in its own rest frame).

There's a good quotation in the book SR by Helliwell that if spacetime is not Newtonian, then we need to revisit all the physics that was derived using Newtonian space and time. We cannot assume that all the non-relativistic formulas for energy, momentum, angular momentum and the motion of springs or ropes remain unchanged.

Yes tottaly true. But is the paradox thath show the need to use relativistic hooke law.
nnnn b

"Length contraction" is frame dependent, and frame dependent quantities have no physical meaning. Actual physics is done with invariants, things that don't depend on which frame you choose.

The invariant that explains why the string in the Bell's spaceship paradox scenario gets stressed is the expansion scalar being positive.

surely you can prove that it is the expansion factor. But what Bell says is that what is responsible is the possibility of always maintaining the same distance in the ground system despite the contraction observed from the ground.The contraction observed from the ground is an invariant.

 

[PeterDonis]

surely you can prove that it is the expansion factor.

If you mean you agree that the expansion scalar of the Bell congruence of worldlines can be proved to be positive, yes, indeed it can.

But what Bell says is that what is responsible is the possibility of always maintaining the same distance in the ground system despite the contraction observed from the ground.The contraction observed from the ground is an invariant.

There is no "contraction observed from the ground". Observed from the ground, the length of the string between the ships remains constant--it does not contract. In order to even use length contraction in this scenario, you have to talk about abstractions like the "unstressed length" of the string. That's basically what Bell's reasoning did.

However, the expansion scalar is a much more straightforward way of getting to the same conclusion, which does not require inventing anything or talking about "contraction" of a string whose actual length does not contract.