Bell's theorem claimed to be refuted - paper published by EPL

[emuc]

The paper says:
Model assumption MA3: Selected photons from each wing of the singlet state which would take a polarizer exit α have polarization

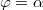. With a selection other than the initial context, all information about the origin from the initial context is lost.

A selection comprises all photons which take the same polarizer exit. Photons with polarization α and

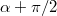come in equal shares, due to symmetry. MA3 accounts for the fact that the polarization of photons from the singlet state is undefined (due to indistinguishability) but changed and redefined by entanglement. Thus, the photons of a selection cannot be distinguished by their polarization. For a selection of the initial states 0° or 90°, the polarization is not changed as it is already equal to the selected state.
MA3 is a contextual assumption, as the polarization of a selection coincides with the setting of a polarizer. It does not imply any restriction on the free choice of the experimenter, nor the dependence of the hidden variable λ on the setting of the measurement instruments. However, it is a local realistic assumption, as it assigns a real value to the physical quantity polarization.

What is unfair with this?

 

[stevendaryl]

I don’t completely understand how this selection is supposed to work. But that’s why I think that the computer simulation clarifies things.

Computer C will simulate the creation of an entangled pair of particles.

It sends a message to A giving all the relevant information about the first particle. It sends a message to B giving all the relevant information about the second particle.

The operators of A and B choose detector settings without consulting each other or the messages from C.

Finally, the program on A computes a result (spin up/ spin down or pass/no-pass or whatever) based on its message and setting, and the program on B analogously computes its result.

So what is the twist that allows the results to match the quantum predictions?

Your specification was

you have to implement the contextual condition that all photons selected by a polarizer set to beta at side B have the polarization beta before selection

I don’t understand what that means. The polarization, along with any other properties of the particle, is specified by computer C. But the choice of detector setting is made by the operator of B. How can the program on B insure that the particle had polarization beta before the selection?

 

[emuc]

Read Model assumption MA3 carefully. This is an assumption how nature is supposed to work. And it is physically justified by the indistinguishability. With this assumption the QM prediction can be reproduced. Entangled photons are not marbles with fixed properties. We have to adapt our assumption about nature in such a way that it can explain the measurement results.
This was also the case with the Einstein-Bode condensate.

 

[stevendaryl]

I don’t understand what that means. The polarization, along with any other properties of the particle, is specified by computer C. But the choice of detector setting is made by the operator of B. How can the program on B insure that the particle had polarization beta before the selection?

Now, I am not sure whether “fair sampling” means what I think it means, but for EPR there is a loophole to Bell’s inequality having to do with failed detections. I’m not sure how it would work with photons, so let me discuss the electron/positron pair version of EPR.

You have a source of entangled pairs. For each pair, you measure the spin of each particle. In practice, some fraction of the measurements will fail, because one detector or the other will fail to detect any particle at all. In the simplest way of handling these failures, we just ignore the results from rounds where only one particle is detected.

However, it might be that the failures are not completely random, but that for certain combinations of detector setting plus hidden variable, failures are more or less likely. We could reproduce the predictions of quantum mechanics by fiddling with the failure probability.

 

[emuc]

I'm not dealing with loopholes.
The polarization is not specified by Computer C.
You asked: "How can the program on B insure that the particle had polarization beta before the selection?"
This is given by the polarizer setting beta. See MA3 above.
Matching events occur for all photons 2 with polarization beta which would hit a polarizer on side B set to alpha+pi/2. Those photons 2 have a peer witch would hit polarizer A set to alpha. That can easily be implemented in a computer system.

 

[stevendaryl]

I'm not dealing with loopholes.
The polarization is not specified by Computer C.
You asked: "How can the program on B insure that the particle had polarization beta before the selection?"
This is given by the polarizer setting beta. See MA3 above.
Matching events occur for all photons 2 with polarization beta which would hit a polarizer on side B set to alpha+pi/2. Those photons 2 have a peer witch would hit polarizer A set to alpha. That can easily be implemented in a computer system.

Sorry, I can’t make any sense of what you are saying. Maybe you could just go through a few example rounds of EPR, and for each round, say what the hidden variable is for that round, what the detector settings are, and what the results are?

 

[PeterDonis]

I can’t make any sense of what you are saying.

You're not the only one.

@emuc, you do not appear to be responding at all to the actual question @stevendaryl is asking. He is asking whether a set of computer programs constructed as described in his post #10 can reproduce the predictions of your model. That is a simple yes or no question which should have a simple yes or no answer.

If your model can produce predictions which violate the Bell inequalities, the answer to the above question should be "no". But if the answer is "no", then your model does not satisfy the assumptions of Bell's Theorem, so the existence of your model does not "refute" Bell's Theorem as you claim it does.

If, OTOH, you claim that your model does satisfy the assumptions of Bell's Theorem (which it would have to for your model's predictions to "refute" Bell's Theorem by violating the Bell inequalities), then the answer to the above question should be "yes"--and you should be able to describe to us how a set of computer programs constructed as described in post #10 can reproduce the predictions of your model, which you claim violate the Bell inequalities.

So which is it? Yes or no?

 

[Nullstein]

I thought it was assumed in the hidden variables, $\lambda$. Those are supposed to contain whatever variables, other than the angles at which the two measurements are made, affect the measurement results.

Leaving the angles to be external parameters not determined by the theory is the "no superdeterminism" assumption.

No, there's a subtle difference. If you leave the angles as external parameters, the model has pre-determined values for all observables, including those that aren't measured. This is enough to enforce Bell's inequality, independent of whether the angles are actually determined or chosen freely.

However, you can relax this condition and only require those observables to be pre-determined that are actually measured. It is only in this case, where an additional "no superdeterminism" assumption is necessary to enforce the inequality. I.e. contextual theories can escape Bell's inequality in principle if no additional assumptions are made ("no superdeterminism").

I bothered to study it in some detail few mounts ago and even to discuss it with her. It turned out that her model is not local.

Did she agree with you? It seems like she still advocates her paper.

But anyway, there can't be any doubt that the "no superdeterminism" assumption is necessary. Even Bell has no problem openly admitting it and people like Spekkens or Zeilinger agree. One can litterally point to an equation in his paper, where he assumes it (eq. 12 in La nouvelle cuisine) and explains that it is necessary, agreeing that his collegues were right. If that can't convince you, I don't know what could.

 

[PeterDonis]

you can relax this condition and only require those observables to be pre-determined that are actually measured. It is only in this case, where an additional "no superdeterminism" assumption is necessary to enforce the inequality.

I'm not sure I understand: only requiring predetermined values for observables that are actually measured is superdeterminism, isn't it? You're basically fine-tuning the model so that it's impossible for any measurements to occur other than the ones that actually occur--i.e., you're predetermining which measurements occur.

 

[emuc]

You're not the only one.

@emuc, you do not appear to be responding at all to the actual question @stevendaryl is asking. He is asking whether a set of computer programs constructed as described in his post #10 can reproduce the predictions of your model. That is a simple yes or no question which should have a simple yes or no answer.

If your model can produce predictions which violate the Bell inequalities, the answer to the above question should be "no". But if the answer is "no", then your model does not satisfy the assumptions of Bell's Theorem, so the existence of your model does not "refute" Bell's Theorem as you claim it does.

If, OTOH, you claim that your model does satisfy the assumptions of Bell's Theorem (which it would have to for your model's predictions to "refute" Bell's Theorem by violating the Bell inequalities), then the answer to the above question should be "yes"--and you should be able to describe to us how a set of computer programs constructed as described in post #10 can reproduce the predictions of your model, which you claim violate the Bell inequalities.

So which is it? Yes or no?

The answer is no. Bell's theorem is refuted because his assumptions about which models are possible are incomplete. He only regarded non-contextual models but didn't take into account contextual models. With his incomplete assumptions he concluded local models were impossible.

 

[emuc]

Sorry, I can’t make any sense of what you are saying. Maybe you could just go through a few example rounds of EPR, and for each round, say what the hidden variable is for that round, what the detector settings are, and what the results are?

I think that's asking a little too much now. You can calculate all of this yourself if you use the publication as a guide.

 

[PeroK]

I suspect that if classical physics predicted there are a finite number of prime numbers and QM predicted an infinite set of primes, then we'd be arguing about it. And the elementary proof of the infinite set of primes would "refuted" by some local realist or other.

 

[stevendaryl]

But anyway, there can't be any doubt that the "no superdeterminism" assumption is necessary.

We can easily generate a local hidden superdeterministic hidden variable theory that reproduces the QM predictions of EPR. In the spin-1/2 version,

Let $\alpha_j$ and $\beta_j$ be sequences of detector orientations. Let $\theta_n$ be the angle between $/alpha_j$ and $/beta_j$. Let $A_n$ be a random sequence of $\pm 1$. Let $B_j$ be a sequence of values chosen so that with probability $sin^2(\theta_j/2)$, it is equal to $A_j$ and with the complementary probability, is the negative of that.

Then we just let the hidden variable for the first particle be $A_j$ and the hidden variable for the second variable be $B_j$. The result is just the value of the hidden variable.

Then if the choices for the two detector settings just happen to be equal to the sequences $\alpha$ and $\beta$, then the statistics will work out as predicted by QM. The hard part is knowing those sequences ahead of time.

 

[Nullstein]

I'm not sure I understand: only requiring predetermined values for observables that are actually measured is superdeterminism, isn't it? You're basically fine-tuning the model so that it's impossible for any measurements to occur other than the ones that actually occur--i.e., you're predetermining which measurements occur.

No, by that definition, Bohmian mechanics would also be superdeterministic. Just think of a Stern-Gerlach apparatus for example. You can only align it along one axis and measure the spin along that axis. When the apparatus is aligned along that axis, it is impossible to measure the spin along any other axis. Now the question is: Is the spin along the other axis determined nevertheless by the model? If yes, then the model is said to be non-contextual. If no, this just means that the result of the measurement is a composite property of the particle and the measurement apparatus, which is perfectly sensible. But still, in an ordinary world, we would not expect violations of Bell's inequality by such a model. However, it is in principle possible to design the theory in such a way that the composite property (particle information + detector alignment) violates Bell's inequality, by making the detector alignment and the particle information depend on each other in a fine-tuned way. This is what has to be excluded and this exclusion is only relevant if we are talking about a contextual model in the first place.

 

[PeterDonis]

The answer is no.

Ok. But then:

Bell's theorem is refuted because his assumptions about which models are possible are incomplete.

This is not what "refuted" means. "Refuted" means the theorem's conclusions do not follow from its assumptions. You are not saying that. So you are not refuting his theorem.

 

[PeterDonis]

The claim made in the title of this thread has been admitted by the OP to be false. Thread closed.