- #1
Bending moment diagram for overhanging beam
- Thread starter David Lewis
- Start date
In summary, the conversation discusses the process of constructing a bending moment diagram for an airplane wing spar. It is mentioned that if the upward force components are equal, it can be simplified as a uniform distributed load (UDL), while if they are different and varying gradually, it can be considered as a varying load (UVL). The formula for calculating the bending moment is also mentioned, using the magnitudes and locations of the forces.
- #2
lingesh
- 28
- 2
If those upward force components F1...Fn are equal in magnitude,then you can simplify it as UDL. If they are different and varying gradually you can consider it as UVL and solve the problem.
- #3
David Lewis
- 846
- 258
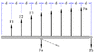
Thanks for your reply. The spar sees a distributed load -- the load diagram is a semi-ellipse. I approximated the distributed load as point loads. I'd like to know the formula to calculate the bending moment, e.g. F1 * d + F2 * 2d...
- #4
FAQ: Bending moment diagram for overhanging beam
1. What is a bending moment diagram for an overhanging beam?
A bending moment diagram is a graphical representation of the internal forces acting on a beam at various points along its length. It shows the bending moment, which is the amount of force that causes a beam to bend, at different points along the beam.
2. How is a bending moment diagram for an overhanging beam calculated?
A bending moment diagram is calculated using the equations for shear force and bending moment. The shear force is the sum of all the external forces acting on the beam at a given point, and the bending moment is the product of the shear force and the distance from that point to the end of the beam.
3. What information can be obtained from a bending moment diagram for an overhanging beam?
A bending moment diagram can provide information about the maximum bending moment, maximum shear force, and location of these maximum values on the beam. It can also show the points where the shear force and bending moment are zero, called the points of contraflexure.
4. How does the shape of an overhanging beam affect its bending moment diagram?
The shape of an overhanging beam can significantly impact its bending moment diagram. Beams with different cross-sectional shapes, such as rectangular, circular, or I-beam, will have different bending moment diagrams. The length and support conditions of the beam will also affect its bending moment diagram.
5. What are the practical applications of understanding the bending moment diagram for an overhanging beam?
Understanding the bending moment diagram for an overhanging beam is essential for designing and analyzing structures. It can help engineers determine the appropriate size and shape of beams for different types of structures and ensure that they can withstand the expected loads. It is also crucial for identifying potential weak points in a structure to prevent failure.