- #1
CompactDisc
- 4
- 0
Hey guys,
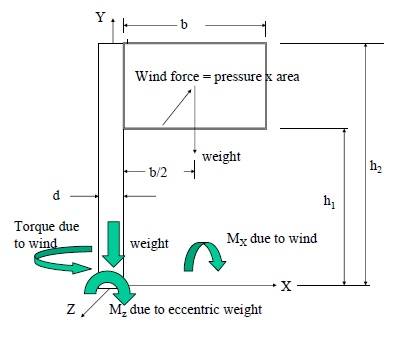
So just completed a question on a sign post subject to wind loading of 2 kPa where you had to determine bending moments across x and z planes (picture below), to determine normal, shear, max stresses and then determine the factor of safety depending on the beam type you chose. That's all good.
The next question is to do with the same problem but now rather than a single beam holding the sign up, there is a beam either side! Moment about x was relatively similar, just slightly larger area and displaced across the two beams but I am stumped with the moment about z. The weight of the sign is now in equilibrium and in the previous problem Mz = weight of the sign * moment arm.
Is Mz now just negligible (equal to 0), or does Mz halve and get spread across the two beams? Any help would be fantastic! And was also unsure where to post this.
So just completed a question on a sign post subject to wind loading of 2 kPa where you had to determine bending moments across x and z planes (picture below), to determine normal, shear, max stresses and then determine the factor of safety depending on the beam type you chose. That's all good.
The next question is to do with the same problem but now rather than a single beam holding the sign up, there is a beam either side! Moment about x was relatively similar, just slightly larger area and displaced across the two beams but I am stumped with the moment about z. The weight of the sign is now in equilibrium and in the previous problem Mz = weight of the sign * moment arm.
Is Mz now just negligible (equal to 0), or does Mz halve and get spread across the two beams? Any help would be fantastic! And was also unsure where to post this.