Bernoulli and Momentum Disconnect?

[erobz]

I was playing around, and I found something unexpected. If we are analyzing a simple fluid jet:

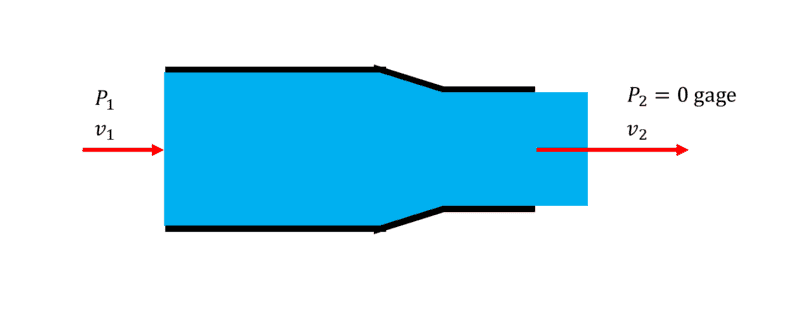
We can apply Bernoulli's (which is Conservation of Energy) and arrive at:

$$ P_{1_{B}} = \frac{1}{2} \rho \left( v_2^2 - v_1^2 \right) = \frac{1}{2} \rho ( v_2 - v_1 ) ( v_2+ v_1) $$

It would seem you could also use the Momentum Equation:

$$ \sum \boldsymbol F = \frac{d}{dt} \int_{cv} \boldsymbol v \rho~dV\llap{-}+ \int_{cs} \boldsymbol v \rho \boldsymbol V \cdot d\boldsymbol A $$

Which says in words:

$$ \left[ \begin{array} ~sum~ of~ forces \\ ~acting ~on ~matter \\ ~in~ control ~volume \end{array} \right] = \left[ \begin{array}~time ~rate~ of \\ ~change ~of~ momentum \\ ~in ~control ~volume \end{array} \right] + \left[ \begin{array} ~ net ~outflow~ rate \\ ~of ~momentum \\ ~through~ control ~surface \end{array} \right]$$

Assuming constant properties across the control surface and steady flow (changing only in position, not time) for that nozzle its reduced to:

$$ P_{1_{M}} = \rho v_1 ( v_2 - v_1) $$

Comparing the two taken independently you get differing results for $P_1$

$$ \frac{P_{1_{M}} }{P_{1_{B}}} = \frac{\rho v_1 ( v_2 - v_1)}{\frac{1}{2} \rho ( v_2 - v_1 ) ( v_2+ v_1)} = \frac{v_1}{\frac{1}{2} ( v_2 + v_1 )}$$

This implies that:

$$ P_{1_{M}} < P_{1_{B}}$$

I guess the difference comes from the fact that I've subtlety left out something in the momentum analysis. In order for the control volume to not be accelerating there must be a force acting on the nozzle in the momentum analysis that was not taken into account, perhaps this is where the discrepancy lies? I notice that in my fluids text they use momentum to solve for the force acting on the nozzle to keep it in place, by first invoking Bernoulli's to solve for the velocities $v_1,v_2$ given pressure $P_1$.

 

[erobz]

Yeah, I think I solved my own problem by trying to explain it. The momentum equation is actually given by:

$$P_{1_{M}} A_1 - F_{restraint} = \rho A_1 v_1 ( v_2-v_1)$$

That added force of restraint would be necessary to keep the cv from accelerating and would act to increase the value of $P_{1_{M}}$.

 

[boneh3ad]

Consider that the Bernoulli equation is simultaneously a conservation of momentum and energy equation. It can be derived directly from the more general versions of each.

For example, if you start with the 1-D, incompressible Euler equation (e.g. taken along a streamline)
\rho u\;du = -dp
you can pretty straightforwardly integrate both sides between two stations 1 and 2
\rho\int_1^2 u\;du = -\int_1^2 dp
\left.\dfrac{\rho u^2}{2}\right|^2_1 = -p|^2_1
\dfrac{\rho u_2^2}{2} + p_2 = \dfrac{\rho u_1^2}{2} + p_1

 

[erobz]

Consider that the Bernoulli equation is simultaneously a conservation of momentum and energy equation. It can be derived directly from the more general versions of each.

For example, if you start with the 1-D, incompressible Euler equation (e.g. taken along a streamline)
\rho u\;du = -dp
you can pretty straightforwardly integrate both sides between two stations 1 and 2
\rho\int_1^2 u\;du = -\int_1^2 dp
\left.\dfrac{\rho u^2}{2}\right|^2_1 = -p|^2_1
\dfrac{\rho u_2^2}{2} + p_2 = \dfrac{\rho u_1^2}{2} + p_1

Ok, so "The Momentum Equation" is apparently not both momentum and energy arguments simultaneously, and that must then have something to do with the treatment of a control volume as opposed to the treatment of streamline, because in the beginning both the Euler and "The Momentum Equation" are variations of Newtons Second Law?

 

[Chestermiller]

Yeah, I think I solved my own problem by trying to explain it. The momentum equation is actually given by:

$$P_{1_{M}} A_1 - F_{restraint} = \rho A_1 v_1 ( v_2-v_1)$$

That added force of restraint would be necessary to keep the cv from accelerating and would act to increase the value of $P_{1_{M}}$.

That added force is the axial component of the force exerted by the wall of the converging nozzle on the flowing fluid.