gamecult
- 8
- 0
- Homework Statement
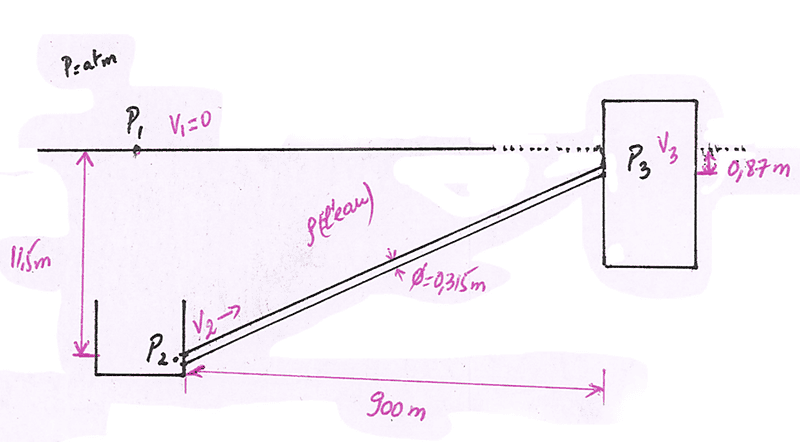
- A seawater collection system consists of two tanks connected by pipe 900m long and 31.5cm in diameter
The pipe inlet is on the seabed at a level of -11.5m and the pipe outlet to Tank 2 is on the beach at a level of -0.875m.
Calculate in detail the water velocity and water flow at the outlet
Both point 1 and 3 are in open aire (Only under atmospheric pressure).
See the drawing for more explanation.
- Relevant Equations
- P_1+1/2 ρv_1^2 + ρgh_1 = P_3+1/2 ρv_3^2 + ρgh_3
Hello everyone;
Please need some help to check if my calculation are correct (and if possible some explantation)
Bernoulli's equation between point 1 and 3 is given by:
Please need some help to check if my calculation are correct (and if possible some explantation)
Bernoulli's equation between point 1 and 3 is given by:
P_1+1/2 ρv_1^2 + ρgh_1 = P_3+1/2 ρv_3^2 + ρgh_3
| P_1 = P_(atm ) v_1= 0 m/s h_1= 0.875 m | P_3 = P_(atm ) v_3= ? m/s h_3= 0 m |
P_(atm )+1/2 ρ(0 m/s)_1^2 + ρg(0.875 m) = P_(atm )+1/2 ρv_3^2 + ρg(0 m)
ρg(0.875 m)=1/2 ρv_3^2
(9,81 m/s^2 )(0.875 m)=1/2 v_3^2
v_3=4.10 m/s
In our case, the pipe diameter is d = 0.315 m (31.5 cm), so the section is:ρg(0.875 m)=1/2 ρv_3^2
(9,81 m/s^2 )(0.875 m)=1/2 v_3^2
v_3=4.10 m/s
A = π × (0.315/2)^2 = 0.0779 m^2
The volume flow Q is then:Q = A×v_3 = 0.0779 m^2 × 4.10 m/s = 0.320 m^3/s
To convert flow from m^3/s to m^3/s
Q = 0.320 m^3/s * 3600 s/h = 1.152 m^3/h
To convert flow from m^3/s to m^3/s
Q = 0.320 m^3/s * 3600 s/h = 1.152 m^3/h
Last edited: