Best fit to an oscillating function

[kelly0303]

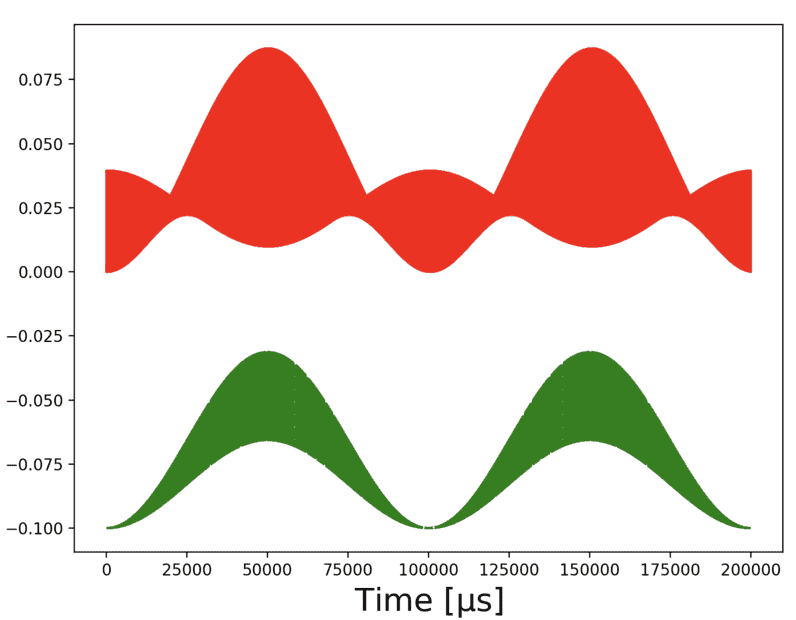
Hello! I have a plot of a function, obtained numerically, that looks like the red curve in the attached figure. It is hard to tell, but if you zoom in enough, inside the red shaded area you actually have oscillations at a very high frequency, $\omega_0$. On top of that you have some sort of envelope, with a lower frequency, $\omega_1$. I am trying to find a function that comes as close as possible to this. In green is what I obtained using:

$$A\sin(\omega_1 t/2)^2(1+\cos(\omega_0t/2))^2$$
where $A$ is just an overall amplitude (and I shifted everything for clarity). However I am not sure how to get the rest of the behaviour, basically fill in the gaps in my function relative to the red one. Can someone advice me on what functional form would I need to add to my expression to get that? Thank you!

 

[DaveE]

Have you considered a Fourier transform?

 

[kelly0303]

Have you considered a Fourier transform?

Thank you! What exactly do you mean? Fourier transform of what?

 

[DrClaude]

Thank you! What exactly do you mean? Fourier transform of what?

Fourier transform of your original signal. It will tell you how to write it as a sum of sines and cosines. If you absolutely to have it as an envelope times a constant oscillation, it will take a bit more work.

If you don't mind sharing the data (at least privately), I would like to take a go at it.

 

[kelly0303]

Fourier transform of your original signal. It will tell you how to write it as a sum of sines and cosines. If you absolutely to have it as an envelope times a constant oscillation, it will take a bit more work.

If you don't mind sharing the data (at least privately), I would like to take a go at it.

Ah I see, thank you I will look into that. There is no actual data. The red-line is generated by numerically integrating on ODE, but I am attaching below the points used in that plot.

 

[Swamp Thing]

If each low-frequency cycle contains thousands (or even hundreds) of high frequency cycles, you may have numerical problems with the Fourier transform. You will have to process way more samples than are really needed to answer your question.

Instead, shift the signal down so that your $\omega_0$ is lower, keeping your $\omega_1$ structure the same. (Then when you plot it, you will be able to see, let's say 20 cycles of $\omega_0 /2$ within one cycle of $\omega_1$. After this down shift the signal will be more amenable to Fourier transform with a moderate number of samples.

You can down shift the "carrier" frequency by multiplying the original signal by $e^{-\omega_2 t}$ where $\omega_2$ is a few percent less than $\omega_0$.

Edit:
As hutchpd has said, you need an 'i' in the exponential.

Downshifting will be a bit more complicated than I have indicated above... I will post later with more details, or maybe someone can fill in the details.

 

[hutchphd]

You need an "i" in the exponential yes?

 

[Swamp Thing]

You need an "i" in the exponential yes?

Yup.

Edit: Wait, I believe there was an i in the original... But anyway.

 

[Swamp Thing]

It will probably work if you just take every 10th or 100th sample (leaving you with say 20 samples per "big" cycle) and pretend that's your actual signal.

 

[Swamp Thing]

Just for fun, I asked Mathematica to find the edges in the OP's plot:

I am now trying to find out if Mathematica can convert the bitmap edges to vectors. Any ideas?

Also, is it correct that the desired low freq. signal is the average of the upper and lower boundaries of the outlines above?