- #1
Mark Sullivan
- 23
- 0
One of the debates in part of the bicycling community is whether elliptical or non round chain rings cause a crank based power meter to over report power beyond the power meters accuracy rate when velocity is only measured once per revolution. Average and weight average of the velocity per revolution plays apart on this position.
The counter argument non round chain rings are just an increase/decrease in the lever and power is coming from your foot on the pedal which is on a circular radius going around a circular axis.
The accuracy of some power crank based power meter is report as +/- 2%. SRM +/-1% accuracy is considered the gold standard in bicycle power meter. The strain gauges are located between the pedal and the chain rings. Velocity is measured by a simple magnet and reed switch once per revolution.

From SRM power meter manufacture http://www.srm.de/:
We have had an increasing number of customers use Q-rings with their SRM Power Meter. There is no difference in wattage accuracy between using a regular chain ring or an elliptical chain ring. The important thing is that the SRM power meter is calibrated with a regular round chain ring to determine the slope of the power meter, which is exclusive to that power meter. Once this is determined, any type of chain ring can be used and wattage accuracy is maintained. Think of it in these terms, the elliptical chain ring only adds more leverage, which in turn can allow for more torque per pedal revolution. This is no more different than changing the crank arm length, which has no effect on the accuracy of the power meter. Torque is torque; and if you can spin the same cadence with the Q-rings, then in theory you will produce more power. We have found from reports of our customers using the q-rings that their cadence tends to drop about 5-10 rpm at a given power output over using regular round chain rings.
This makes the most sense to me as the only power to propel the bike forward is coming from your foot and there are a number of levers and opposing forces that can change cadence.
The best opposing argument comes from a Mechanical Engineer Tom Anhalt http://bikeblather.blogspot.com.au/2013/01/whats-up-with-those-funky-rings.html There is a picture of one manufacture’s of these non round ring (Osymetric chainrings). He does a comparison experiment towards the end of the blog.

Osymetric Chainrings with SRM Powermeter
I have a number of questions about his blog but one in particular is on how he calibrated. “Calibration shows the Round ring (mounted on the outer position) reads 1% high and the Osymetric (mounted on the inner position) reads 1% low and the torque slope was set to the average value between the 2 rings. Power values from the Quarq reported below were corrected based on the calibration.”
All end user calibration spreadsheets are based on round rings to figure out the lever length so he doesn’t explain how he determined the lever length of the Osymetric chainrings. Also just doing the calibration with the round chainring 3 times, and averaging the values should be sufficient enough for both rings. SRM points out. His way seems to allow more room for error and question.
The funny thing is that these non round rings are sold as: “because of their pseudo-elliptical shape, Osymetric rings concentrate your pedaling power where your force is at a maximum, while effectively reducing the load where your power input is at a minimum.” “It works on the objective of minimizing the time spent in dead spots, while maximizing the time spent within the radii of efficient power exertion -- horizontal. Basically, this means that, as the operator, you can apply more force while spending less energy. In fact, Osymetric's design minimizes torque and effort by creating a nearly constant angular velocity.”
“apply more force while spending less energy” is a red flag for me. And than nearly constant angular velocity, I thought the problem was non round ring had a varied velocity compared to round rings during each revolution.
There also seems to be the assumption that with round rings the velocity of the pedal/crank is fairly constant or maybe they know that.
My take is that non round rings just move force and velocity around and that work is work.
Thanks for your comments and insights.
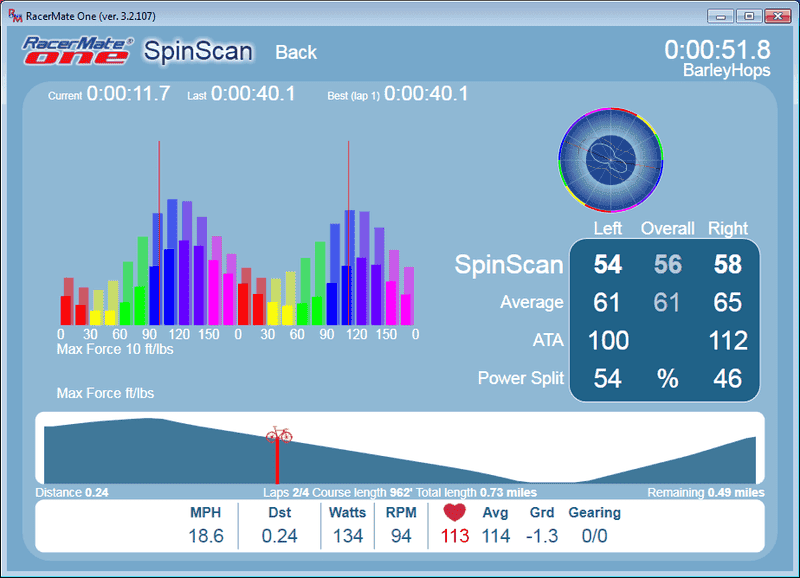
Typical power distribution on round chainrings
The counter argument non round chain rings are just an increase/decrease in the lever and power is coming from your foot on the pedal which is on a circular radius going around a circular axis.
The accuracy of some power crank based power meter is report as +/- 2%. SRM +/-1% accuracy is considered the gold standard in bicycle power meter. The strain gauges are located between the pedal and the chain rings. Velocity is measured by a simple magnet and reed switch once per revolution.
From SRM power meter manufacture http://www.srm.de/:
We have had an increasing number of customers use Q-rings with their SRM Power Meter. There is no difference in wattage accuracy between using a regular chain ring or an elliptical chain ring. The important thing is that the SRM power meter is calibrated with a regular round chain ring to determine the slope of the power meter, which is exclusive to that power meter. Once this is determined, any type of chain ring can be used and wattage accuracy is maintained. Think of it in these terms, the elliptical chain ring only adds more leverage, which in turn can allow for more torque per pedal revolution. This is no more different than changing the crank arm length, which has no effect on the accuracy of the power meter. Torque is torque; and if you can spin the same cadence with the Q-rings, then in theory you will produce more power. We have found from reports of our customers using the q-rings that their cadence tends to drop about 5-10 rpm at a given power output over using regular round chain rings.
This makes the most sense to me as the only power to propel the bike forward is coming from your foot and there are a number of levers and opposing forces that can change cadence.
The best opposing argument comes from a Mechanical Engineer Tom Anhalt http://bikeblather.blogspot.com.au/2013/01/whats-up-with-those-funky-rings.html There is a picture of one manufacture’s of these non round ring (Osymetric chainrings). He does a comparison experiment towards the end of the blog.
Osymetric Chainrings with SRM Powermeter
I have a number of questions about his blog but one in particular is on how he calibrated. “Calibration shows the Round ring (mounted on the outer position) reads 1% high and the Osymetric (mounted on the inner position) reads 1% low and the torque slope was set to the average value between the 2 rings. Power values from the Quarq reported below were corrected based on the calibration.”
All end user calibration spreadsheets are based on round rings to figure out the lever length so he doesn’t explain how he determined the lever length of the Osymetric chainrings. Also just doing the calibration with the round chainring 3 times, and averaging the values should be sufficient enough for both rings. SRM points out. His way seems to allow more room for error and question.
The funny thing is that these non round rings are sold as: “because of their pseudo-elliptical shape, Osymetric rings concentrate your pedaling power where your force is at a maximum, while effectively reducing the load where your power input is at a minimum.” “It works on the objective of minimizing the time spent in dead spots, while maximizing the time spent within the radii of efficient power exertion -- horizontal. Basically, this means that, as the operator, you can apply more force while spending less energy. In fact, Osymetric's design minimizes torque and effort by creating a nearly constant angular velocity.”
“apply more force while spending less energy” is a red flag for me. And than nearly constant angular velocity, I thought the problem was non round ring had a varied velocity compared to round rings during each revolution.
There also seems to be the assumption that with round rings the velocity of the pedal/crank is fairly constant or maybe they know that.
My take is that non round rings just move force and velocity around and that work is work.
Thanks for your comments and insights.
Typical power distribution on round chainrings