Biomedical Engineering: Scanning k-space in NMR with readout gradient

[Master1022]

TL;DR Summary

How does applying the gradient coils after the initial RF pulse help to encode information in x and y directions in our chosen slab?

Hi,

Firstly, I apologize if this is the wrong forum to post this. I am learning about this concept in a biomedical engineering context, but perhaps this may be better suited to the Biology or Physics pages. If so, please let me know and I can move the post.

In short, I am confused how we can use the gradient coils, after the initial RF pulse, to scan k-space when taking an NMR.

Here is what I understand:

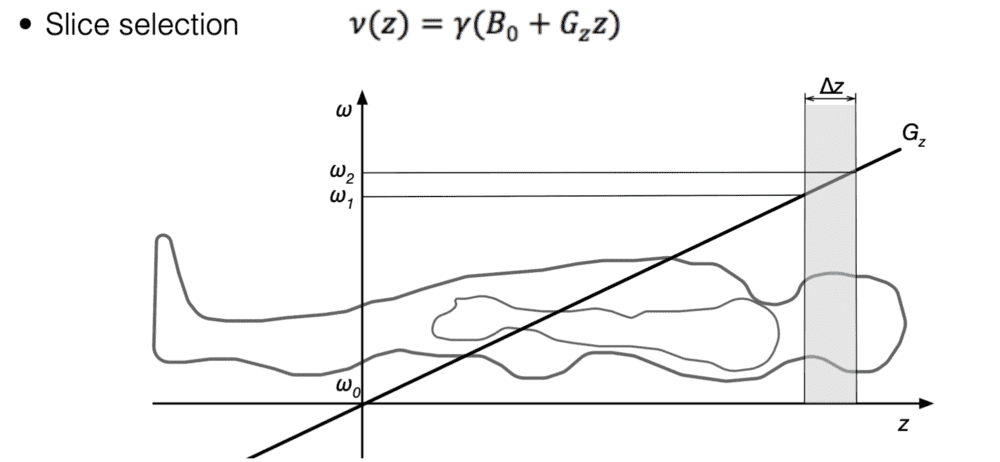
1. We can apply an gradient in the z-direction to make the Lamor frequency a function of z. This allows us to select a certain slice by applying any range of frequencies for our RF pulse.

2. Now that we have a slice/slab, we want to get information more specifically from different points in the x-y plane. Therefore we apply a readout gradient. My main misunderstanding is how this helps us.

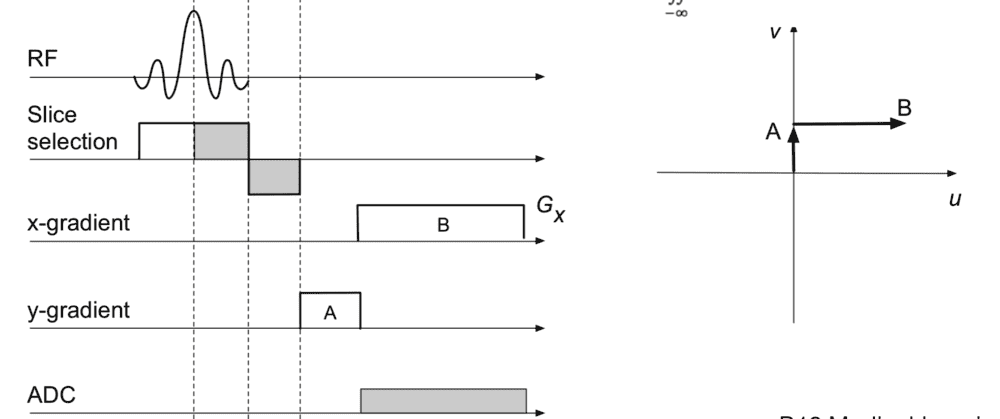
Question 1: How does the readout gradient help us traverse x-y space? It looks like the gradient pulses move us in the $u$ and $v$ directions in $k$-space (which I understand to basically be Fourier space). From animations of this process, it seems like the readout gradients move us in $k$-space, rather than us moving around manually.

My guess of how this works is that:
- when we apply this gradient coil, this introduces a spatial variation for the Lamor frequency in that same direction (e.g. x-gradient pulse introduces spatial variation in x-direction)
- This then causes an integral (based on the above diagram) for the signal to be (I believe $T_p$ is the time of the y-gradient pulse):

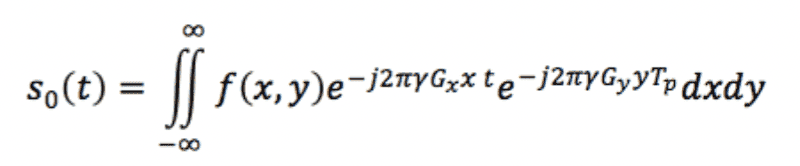
Question 2: Why can we just substitute the $G_x x$ for $u$ and likewise for $v$? I understand that the pulses introduce a variation in the respective directions, but am not sure why that means we can make the substitution.

Any help would be greatly appreciated. I feel that I have one or two core misunderstandings which probably underpin most of these questions.

Thanks

 

[dlgoff]

Since the Larmor frequency of the detected signal is proportional to the applied magnetic field, changing the magnitude of that field produces a different detected frequency. Placing a magnetic field gradient across a sample allows you to locate the source of the proton NMR signal in the sample. This is used to great advantage in the medical imaging process known as Magnetic Resonance Imaging.

Figure 9-25: Comparison of sweep rates on nmr absorption curves; (a) 500-sec sweep, (b) 50-sec sweep, (c) 10-sec sweep, The "ringing" in the faster sweep curves is a transient effect that has a small effect on the position of the peak and none on the integral.

Image compliments of http://hyperphysics.phy-astr.gsu.edu/

 

[Master1022]

Thank you for your reply @dlgoff !

However, I am still slightly confused...

Since the Larmor frequency of the detected signal is proportional to the applied magnetic field, changing the magnitude of that field produces a different detected frequency. Placing a magnetic field gradient across a sample allows you to locate the source of the proton NMR signal in the sample. This is used to great advantage in the medical imaging process known as Magnetic Resonance Imaging.

This part makes sense. When we apply the initial gradient in the z-direction, it helps choose the slab/slice. Then we apply a x-gradient pulse after the initial RF pulse. As you say, this now introduces another spatial dependence for the x direction within that plane. I am still not understanding what the connection between the readout gradient and the k-space scanning is.

Apologies if I am missing something obvious.

 

[dlgoff]

readout gradient

Thank you for your reply @dlgoff !

However, I am still slightly confused...
This part makes sense. When we apply the initial gradient in the z-direction, it helps choose the slab/slice. Then we apply a x-gradient pulse after the initial RF pulse. As you say, this now introduces another spatial dependence for the x direction within that plane. I am still not understanding what the connection between the readout gradient and the k-space scanning is.

Apologies if I am missing something obvious.

Isn't the readout gradient=magnetic field gradient? Not sure I understand what "readout gradient" means here.

 

[Baluncore]

https://en.wikipedia.org/wiki/K-space_(magnetic_resonance_imaging)

 

[Master1022]

Thanks for your reply.

Isn't the readout gradient=magnetic field gradient? Not sure I understand what "readout gradient" means here.

Yes it is a magnetic field. Although I thought the readout gradient was specifically referring to the use of the gradient coils after the RF pulse; so the readout gradient would be to traverse through k-space (if that is what it does? or maybe it is x-y space?), whereas the 'standard' use of the gradient coil was for slice selection.

I am just confused how/why those x-gradient and y-gradient pulses shown in the diagram at the top actually help us move through k-space. I know that they introduce a magnetic gradient which creates a spatial dependence for the lamor frequency. But what is the logical jump from that step to us moving around in k-space? I can see the integral has the $G_x$ and $G_y$, but I wasn't sure how that came about. I hope this better explains where my misunderstanding is. Basically, we have applied those x-gradient and y-gradient pulses - so what?

Thanks for the help

 

[Tom.G]

See:
https://www.mriquestions.com/gradient-echo.html

That whole series seems to do a decent job of explaining MRI subtleties without burying you in the math.

(above found with:
https://www.google.com/search?&q=mri+readout+gradient)

Cheers,
Tom

 

[Master1022]

Thanks @Tom.G ! That website is quite helpful.

See:
https://www.mriquestions.com/gradient-echo.html

That whole series seems to do a decent job of explaining MRI subtleties without burying you in the math.

(above found with:
https://www.google.com/search?&q=mri+readout+gradient)

Cheers,
Tom

I just had one final question about this concept. After reading the website, a few points became clear:
- When we apply the readout gradient, then the lamor frequencies vary with x (or y, depending on the direction of the gradient)
- The points with higher frequencies will accumulate a phase difference over time, with respect to the points with lower frequencies
The one part I cannot understand is on this page here: https://www.mriquestions.com/why-signal-harr-k-space.html and I have put a picture right below of the specific section:

and the text some time below states (only referring to the last paragraph in the image, but have included the rest for context):

Why is it the case that the resultant MR signal at each point in time (t) thus reflects increasing spatial frequencies and the summed phase angles from all locations in the image?
Why would the frequency vary with time if the pulse amplitude is constant (as often shown in these examples)?
- From reading, when the readout gradient is applied, it introduces a variation into the natural resonant Lamor frequency, but I cannot see how that varies with time while the pulse is activeIf I accept that as true, then the next step of the logic seems reasonable. Each point in time on the signal represents a different frequency and phase and thus corresponds to a different point in k-space, which helps us to fill out a row and/or column.

 

[Tom.G]

Why would the frequency vary with time if the pulse amplitude is constant (as often shown in these examples)?

The pulse shown in the diagram indicates the time period that the Gradient field is present, not the amplitide of a fixed pulse.
(another way of describing the diagram is that the pulse is a gating function (or an Enable signal) for the gradient field.)

Since there is a gradient field, the Lamor frequency will vary along the gradient; hence all the frequencies will be present during the gradient presence. When the pulse of Gradient Field ends, the Lamor frequency returns to the value of the quiescent field.

Cheers,
Tom

 

[Master1022]

Thanks for your reply @Tom.G!

Since there is a gradient field, the Lamor frequency will vary along the gradient; hence all the frequencies will be present during the gradient presence.

True, but whilst the gradient is being applied, the Lamor frequency at an individual point will be at its new value, but won't be changing until the pulse turns off.

Does the wording on the page not indicate that there is a temporal variation of the Lamor frequency at a given point in space while the pulse is being applied? I thought the Lamor frequency of an arbitrary point A would start at $\omega_1$, then change to $\omega_2$ when the readout gradient is applied and stay at that exact same value until the gradient stops, at which point it reverts back to $\omega_1$ as you said. Often the examples given are that we introduce a term $G_x x$ and it is usually implied that $G_x$ is a constant. That is why I was confused by the statement: "the resultant MR signal at each point in time (t) thus reflects increasing spatial frequencies"

Where does this signal actually come from (perhaps that is why I am getting confused)? I seem to think it is the current reading from the RF coil in the machine...

When the pulse of Gradient Field ends, the Lamor frequency returns to the value of the quiescent field.

Agreed

 

[Tom.G]

Does the wording on the page not indicate that there is a temporal variation of the Lamor frequency at a given point in space while the pulse is being applied?

Not that I noticed, but I'm really not an expert.

"the resultant MR signal at each point in time (t) thus reflects increasing spatial frequencies"

Confusing, for sure.

I seem to think it is the current reading from the RF coil in the machine...

That is my understanding.

Overall, I think much confusion comes from "the resultant MR signal at each point in time (t) thus reflects increasing spatial frequencies". If you append the phrase "along the gradient.", It all seems to hang together.

See if the equations work with that interpretation, they are beyond my ability to evaluate.

Cheers,
Tom

 

[Baluncore]

Overall, I think much confusion comes from "the resultant MR signal at each point in time (t) thus reflects increasing spatial frequencies". If you append the phrase "along the gradient.", It all seems to hang together.

Take the simplest example. The process starts by polarising the bulk sample for a short period. When the polarisation is removed, relaxation results in precession at the Larmor frequency. A gradient field is then applied to determine the Larmor frequency along some selected 3D axis. The total of the RF is digitised and recorded for a period of time. The FFT of that time record gives the frequency distribution of precession energy present.

Since the gradient field determined the spatial distribution of Larmor frequency, the FFT reveals the spatial distribution of precession energy along the selected gradient axis. That is conceptually K-space.

When discussing the gradient of Larmor frequency, confusion arises when the terms “spatial“ and "frequency” are wrongly conflated. "Spatial frequency" refers to the FFT of a spatial image, which would require a further FFT beyond K-space in NMR.