- #1
VortexLattice
- 146
- 0
Hi everyone!
I'm trying to do the classic calculation of the coefficients of transmission and reflection at a surface, but for a uniaxial crystal. I'm doing the simplest case, in which the optical axis is normal to the reflecting surface. Here is a simple diagram of what I'm trying to do:
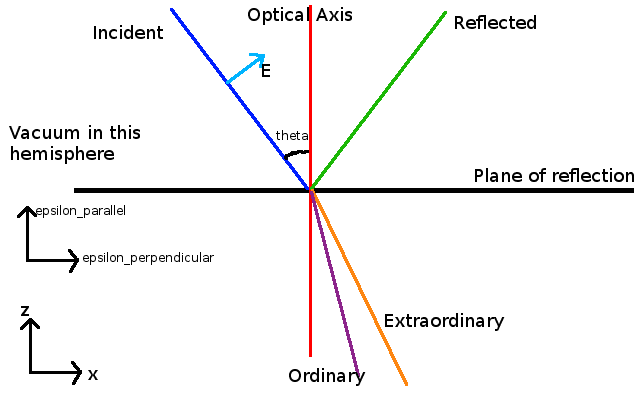
(Sorry if it's messy or cluttered, I didn't want to leave anything out. We're taking the magnetic permeability to be 1, also. I chose the incident wave's E field to be entirely parallel to the plane of incidence because an incident wave with it at any other angle is just a superposition of this wave and one with the E field perpendicular to the plane of incidence, and that case seems easier)
So, I have a bunch of questions that I can't seem answer. Foremost, I know in the special case of the incident wave being normal to the reflecting surface, there is only one transmitted wave. But in all other cases, will there always be both an ordinary (O) and extraordinary (X) wave?
Second, I was reading in Landau and Lifgarbagez' Electrodynamics of Continuous media, the chapter on anisotropic media, and they say that "The vectors [itex]\vec{D}[/itex] in the O and E waves with the same direction of [itex]\vec{k}[/itex] are perpendicular. Hence the polarization of the ordinary wave is such that E and D lie in a plane perpendicular to the principal section" (the principal section is the plane with S (poynting vector), the optical axis, and k).
But this seems to clash with the boundary conditions I know this problem needs to fulfill. We need to have D perpendicular, B perpendicular, E parallel, and H parallel continuous at the boundary. But if the ordinary wave has its E field perpendicular to the E field of the incident wave... well, that can't add up. So what am I missing?
From what I can tell, that quote may be true if the wave vectors of the O and X waves are the same, but they shouldn't be, right? This is what I'm understanding right now: An incident beam comes in. The O wave refracts completely normally, as if it was refracting in an isotropic medium of index of refraction [itex]ε\bot[/itex]. Because it is refracting normally, its polarization is in the same direction (in this case, in the plane of incidence) as the incident wave, and its wave vector and poynting vector have the same direction.
Then, the wave also refracts into the X wave, which has a different wave vector than the O wave's wave vector. However, the poynting vectors and wave vectors of the O and X waves are still all coplanar, right?
Does that seem correct? Can anyone help me??
Thanks!
I'm trying to do the classic calculation of the coefficients of transmission and reflection at a surface, but for a uniaxial crystal. I'm doing the simplest case, in which the optical axis is normal to the reflecting surface. Here is a simple diagram of what I'm trying to do:
(Sorry if it's messy or cluttered, I didn't want to leave anything out. We're taking the magnetic permeability to be 1, also. I chose the incident wave's E field to be entirely parallel to the plane of incidence because an incident wave with it at any other angle is just a superposition of this wave and one with the E field perpendicular to the plane of incidence, and that case seems easier)
So, I have a bunch of questions that I can't seem answer. Foremost, I know in the special case of the incident wave being normal to the reflecting surface, there is only one transmitted wave. But in all other cases, will there always be both an ordinary (O) and extraordinary (X) wave?
Second, I was reading in Landau and Lifgarbagez' Electrodynamics of Continuous media, the chapter on anisotropic media, and they say that "The vectors [itex]\vec{D}[/itex] in the O and E waves with the same direction of [itex]\vec{k}[/itex] are perpendicular. Hence the polarization of the ordinary wave is such that E and D lie in a plane perpendicular to the principal section" (the principal section is the plane with S (poynting vector), the optical axis, and k).
But this seems to clash with the boundary conditions I know this problem needs to fulfill. We need to have D perpendicular, B perpendicular, E parallel, and H parallel continuous at the boundary. But if the ordinary wave has its E field perpendicular to the E field of the incident wave... well, that can't add up. So what am I missing?
From what I can tell, that quote may be true if the wave vectors of the O and X waves are the same, but they shouldn't be, right? This is what I'm understanding right now: An incident beam comes in. The O wave refracts completely normally, as if it was refracting in an isotropic medium of index of refraction [itex]ε\bot[/itex]. Because it is refracting normally, its polarization is in the same direction (in this case, in the plane of incidence) as the incident wave, and its wave vector and poynting vector have the same direction.
Then, the wave also refracts into the X wave, which has a different wave vector than the O wave's wave vector. However, the poynting vectors and wave vectors of the O and X waves are still all coplanar, right?
Does that seem correct? Can anyone help me??
Thanks!
Last edited: