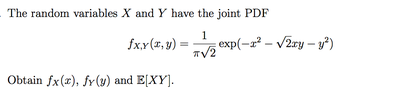- #1
Longines
- 10
- 0
Hello all,
How would I do this question by hand?
I know I integrate from -infinity to +infinity for $f_x,y$, but I have no idea how to do it by hand! My algebra soup is bad, can someone please help me?
View attachment 3237P.S I heard some of my friends talking about some 'trick' you can do with the exponential part of the equation to solve it quicker.. but I don't know what they were talking about.
Thank you
How would I do this question by hand?
I know I integrate from -infinity to +infinity for $f_x,y$, but I have no idea how to do it by hand! My algebra soup is bad, can someone please help me?
View attachment 3237P.S I heard some of my friends talking about some 'trick' you can do with the exponential part of the equation to solve it quicker.. but I don't know what they were talking about.
Thank you