Black hole singularity, a time-like surface?

[Hill]

TL;DR Summary

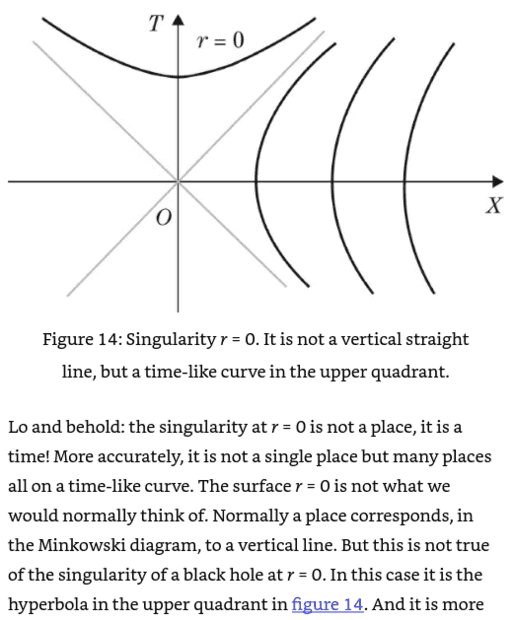
In "General Relativity: The Theoretical Minimum" (Susskind, Leonard; Cabannes, André), the surface corresponding to the black hole singularity is described as time-like. Why?

Below is the description from the book. I thought that hyperbolas in the right quadrant are time-like and hyperbolas in the upper quadrant are space-like. If it were so, the surface $r=0$ would be space-like, but the book says otherwise. -- ?

 

[PeterDonis]

Below is the description from the book. I thought that hyperbolas in the right quadrant are time-like and hyperbolas in the upper quadrant are space-like.

You are correct. The singularity in a Schwarzschild black hole, which is what the diagram is showing, is spacelike. That is a huge error, which I am extremely surprised to see in that book.

 

[PeterDonis]

The singularity in a Schwarzschild black hole, which is what the diagram is showing, is spacelike.

I guess Susskind needs to read Wald, section 6.4, which explicitly states what I state in the quote above.

 

[Ibix]

On a Kruskal diagram, like on a Minkowski diagram, null lines slope at 45° and timelike lines are steeper than that.

The body text correctly notes that the singularity is more like a time than a place, though, meaning it is spacelike (any "now" must be a spacelike surface - or line in the case of the Schwarzschild singularity). So the caption is a typo that's got past the authors and editors.

 

[PeterDonis]

the caption is a typo

At least two of them, since "time-like" appears in both the Figure label and the paragraph of text beneath it.

 

[vanhees71]

On a Kruskal diagram, like on a Minkowski diagram, null lines slope at 45° and timelike lines are steeper than that.

The body text correctly notes that the singularity is more like a time than a place, though, meaning it is spacelike (any "now" must be a spacelike surface - or line in the case of the Schwarzschild singularity). So the caption is a typo that's got past the authors and editors.

In other words, the hypersurfaces $r=\text{const}$ with $r<r_{\text{S}}$ are spacelike since the corresponding $r$-lines are "normal vectors" of this hypersurface are time-like. It's often confusing, but one has to remember that a hypersurface is spacelike if the normalvector is timelike and vice versa. So I'd also say the singularity $r=0$ is a spacelike hypersurface rather than calling it time-like.

 

[martinbn]

May be they meant to say that it is like a moment of time. Many places at the same time.

 

[vanhees71]

But that's indeed a spacelike hypersurface ;-)), but I'm not too harsh with textbook authors concerning typos. Tell me a recipy how to produce typo-free textbooks ;-)).

 

[Hill]

I'd call it "misspoken" rather than "typo". It doesn't matter really. I'm just glad that I've spotted it and that my understanding so far is correct.

 

[PeterDonis]

Many places at the same time.

The text sort of says that, but the correct term for such a surface is "spacelike"--it's a surface that can be viewed as "space"--many places--at an instant of time.

 

[Hill]

Hmm... The book insists: 20 pages later, referring to this figure,

it says,

 

[PeterDonis]

The book insists: 20 pages later, referring to this figure

If by "upper quadrant" they mean the black hole region, this is of course wrong. The constant $t$ lines in the black hole region are timelike, and the constant $r$ hyperbolas are spacelike.

I am skeptical that these were typos. Based on my previous experience reading papers by Susskind, I suspect he is making up his own terminology (where "space-like" means "like a point in space" and "time-like" means "like an instant of time") and either hasn't bothered to check the literature, or doesn't think it matters. Which, given that this book is supposed to be for pedagogy, does not strike me as a sound strategy. I hope I'm wrong.

 

[Hill]

If by "upper quadrant" they mean the black hole region

They do.

his own terminology

Not in this case: earlier in the book he says,

 

[Ibix]

Some terrible search-and-replace disaster?

$t$ is a spacelike coordinate inside the horizon which means that lines of constant $t$ (on this 1+1d diagram) are time-like, and vice-versa outside.

 

[vanhees71]

That's an amazing mistake in a (pre-)introductory textbook then. It's anyway confusing with space-like vs. time-like concerning 3D hypersurfaces (already in SR but the more in GR).

The right local criterion is that a hypersurface is called space-like if the normal vectors are time-like.

In the usual Schwarzschild coordinates for $r<r_{\text{S}}$ the $t$-coordinate is space-like and the $r$-coordinate is time-like (which adds to the confusion, because it's labelled $t$ for "time" and $r$ for "radial coordiante" due to the fact that $t$ is the time-like coordinate and $r$ a space-like coordinate outside the event horizon, i.e., for $r>r_{\text{S}}$).

Now for the hypersurfaces defined by $t=\text{const}$ the lines $(r,\vartheta,\varphi)=\text{const}$, i.e., the $t$-lines are spacelike for $r<r_{\text{S}}$, and they are the "hypersurface normal vectors", and thus these hypersurfaces are time-like.

 

[Nugatory]

Some terrible search-and-replace disaster?

Y'know, the more I think about it the more plausible this hypothesis becomes.

 

[PeterDonis]

earlier in the book he says

In itself that quote could be consistent with standard terminology, since the signs of squared intervals depend on what metric signature convention you adopt. In standard terminology, the quote you give is simply describing the standard timelike signature convention.

But if all he's doing is using the standard timelike signature convention, then he's using it wrong in the other quotes you give. So he can't just be using standard terminology.

 

[Hill]

In itself that quote could be consistent with standard terminology, since the signs of squared intervals depend on what metric signature convention you adopt. In standard terminology, the quote you give is simply describing the standard timelike signature convention.

But if all he's doing is using the standard timelike signature convention, then he's using it wrong in the other quotes you give. So he can't just be using standard terminology.

He uses the standard terminology everywhere else. Here are some examples:

 

[PeterDonis]

He uses the standard terminology everywhere else. Here are some examples

Interesting, so his usage is inconsistent. That would seem to be a point in favor of the "typo" theory.

 

[PeterDonis]

Some terrible search-and-replace disaster?

If it were that one would expect it to show up in the example @Hill gave in post #18, but it doesn't.