Block connected to 2 real pulleys

[Thermofox]

Homework Statement

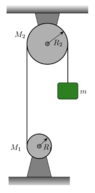
1)Find the acceleration of the hanging block
2)Assuming the system starts at rest, Find the velocity of the block when Pulley 2 completes 2 full revolutions

Relevant Equations

Σ F= ma
Σ τ= Iα

For point one I analyzed all of the forces, called the tension on the right $T_2$ and the left one $T_1$, and taking as positive the clock-wise and upwards directions I found:
$$\begin{cases}
T_2 - mg = ma \\
N_2= T_2 + M_2g + T_1 \\
N_1= M_1g - T_1 \\
τ_{T_2} - τ_{T_1} = I_2 α_2\\
τ_{T1} = I_1 α_1
\end{cases}$$
I solved the system and found that $T_2 = 3a$ thus I have that $3a -mg = 3a$ which doesn't make sense, where did I make the mistake?
The only thing that raises my suspicion are the angular accelerations, Because I considered $$α_1 = \frac a {R_1} ; α_2= \frac a {R_2}$$ I don't know If it is a fair assumption to make.

As for point two genuinely don't know how to do it. I suppose that I would have to use the energetic balance, since the system is conservative. Yet I don't know how to translate into math the 2 revolutions of pulley 2.

 

[kuruman]

The only thing that raises my suspicion are the angular accelerations, Because I considered $$α_1 = \frac a {R_1} ; α_2= \frac a {R_2}$$ I don't know If it is a fair assumption to make.

This is correct. A point on the string has acceleration $a$ which is the same as that of the hanging mass. If the string does not slip at the pulleys (a fair assumption to make), the tangential acceleration at the rim of each pulley should be the same, $a=\alpha_1R_1=\alpha_1R_2.$

$$
\begin{cases}

T_2 - mg = ma -- \text{ Check your signs}\\

N_2= T_2 + M_2g + T_1 -- \text{what does } N_2 \text{ represent and why is it relevant? }\\

N_1= M_1g - T_1 -- \text{what does } N_2 \text{ represent and why is it relevant? }\\

τ_{T2} - τ_{T_1} = I_2 α_2 -- \text{ I would express the torque in terms of the tension}\\

τ_{T1} = I_1 α_1-- \text{ I would express the torques in terms of the tensions}

\end{cases}
$$To see how to proceed with this problem you first need to consider how many unknowns you have and what they are. Then you need to trim the number of your equations to a number equal to the number of your unknowns.

I would use Newton's second law for part (a) and energy considerations for part (b). Energy considerations can also be used for part (a) but are not recommended unless you know what you're doing.

 

[jbriggs444]

At a guess, @Thermofox is considering $N_2$ to be the "normal force" of the upper pulley on its axle. Similarly, $N_1$ is the "normal force" of the lower pulley on its axle.

I agree that neither equation is relevant.

My inclination would be to work with energy rather than acceleration. How much energy is added due to the descent of the mass? How much energy will the system have in terms of the [equal] speeds of the rim of pulley 1, the rim of pulley 2 and the descending mass?

 

[Thermofox]

This is correct. A point on the string has acceleration $a$ which is the same as that of the hanging mass. If the string does not slip at the pulleys (a fair assumption to make), the tangential acceleration at the rim of each pulley should be the same, $a=\alpha_1R_1=\alpha_1R_2.$

$$
\begin{cases}

T_2 - mg = ma -- \text{ Check your signs}\\

N_2= T_2 + M_2g + T_1 -- \text{what does } N_2 \text{ represent and why is it relevant? }\\

N_1= M_1g - T_1 -- \text{what does } N_2 \text{ represent and why is it relevant? }\\

τ_{T2} - τ_{T_1} = I_2 α_2 -- \text{ I would express the torques in terms of the tensions}\\

τ_{T1} = I_1 α_1-- \text{ I would express the torques in terms of the tensions}

\end{cases}
$$To see how to proceed with this problem you first need to consider how many unknowns you have and what they are. Then you need to trim the number of your equations to a number equal to the number of your unknowns.

$$
\begin{cases}

T_2 - mg = -ma -- \text{ Adjusted sign of acceleration}\\

N_2= T_2 + M_2g + T_1 -- N_2~ \text {Is the force generated by the hang of the pulley, so that they stay still. I put it just for completeness, but I don't think it's relevant to solve this problem}\\

N_1= M_1g - T_1 \\

(T_1 - T_2)R_2 = I_2 α_2 -- \text{ Done}\\

T_1 R_1 = I_1 α_1-- \text{Done}

\end{cases}
$$

 

[kuruman]

$$
\begin{cases}

T_2 - mg = -ma -- \text{ Adjusted sign of acceleration}\\

N_2= T_2 + M_2g + T_1 -- N_2~ \text {Is the force generated by the hang of the pulley, so that they stay still. I put it just for completeness, but I don't think it's relevant to solve this problem}\\

N_1= M_1g - T_1 \\

(T_1 - T_2)R_2 = I_2 α_2 -- \text{ Done}\\

T_1 R_1 = I_1 α_1-- \text{Done}

\end{cases}
$$

Right. So the equations involving $N_1$ and $N_2$ can be used to ascertain that the axes of the pulleys are and remain at rest while the mass is dropping.

How many equations and how many unknowns do you have?

 

[Thermofox]

I have 3 unknowns and 5 equations ( 3 if I don't consider $N_1$ and $N_2$).
=> I can solve the system and find:
$T_1 = \frac 1 2 M_1 a$ and $T_2 = \frac 1 2 (M_1 + M_2)a$ therefore,
$a= \frac {mg} {m+\frac 1 2 (M_1+M_2)}$

 

[kuruman]

That doesn't look right. The radii and moments of inertia of the pulleys must be part of the answer. Please post your work.

On edit: Does the problem specify that the pulleys are to be treated as solid cylinders?

 

[Thermofox]

At a guess, @Thermofox is considering $N_2$ to be the "normal force" of the upper pulley on its axle. Similarly, $N_1$ is the "normal force" of the lower pulley on its axle.

I agree that neither equation is relevant.

My inclination would be to work with energy rather than acceleration. How much energy is added due to the descent of the mass? How much energy will the system have in terms of the [equal] speeds of the rim of pulley 1, the rim of pulley 2 and the descending mass?

If set the zero of gravitational potential on m I have that:
$E_{initial}= E_{final}$ => $0= E_{m,gravitational} + E_{m,kinetic} + E_{1, kinetic} + E_{2,kinetic}$

=> $0= mgh + \frac 1 2 mv^2 + \frac 1 2 I_1ω_1 + \frac 1 2 I_2ω_2$. I don't know if there are any relationships between $ω_1$ and $ω_2$

 

[jbriggs444]

I have 3 unknowns and 5 equations ( 3 if I don't consider $N_1$ and $N_2$).
=> I can solve the system and find:
$T_1 = \frac 1 2 M_1 a$ and $T_2 = \frac 1 2 (M_1 + M_2)a$ therefore,
$a= \frac {mg} {m+\frac 1 2 (M_1+M_2)}$

I counted seven unknowns and eight parameters.

Unknowns: $T_1, T_2, a, N_1, N_2, \alpha_1, \alpha_2$
Parameters: $R_1, R_2, M_1, M_2, g, m, I_1, I_2$

Apparently you added two equations: $a = R_1 \alpha_1$ and $a = R_2 \alpha_2$ as suggested by @kuruman without adding those to the equation count.

Apparently you were able to solve the resulting system for $a$ without needing to determine all of the parameters.

That doesn't look right. The radii and moments of inertia of the pulleys must be part of the answer. Please post your work.

It is right. The radii of the pulleys is irrelevant. Only their masses matter.

[Edit: @kuruman properly points out that I am implicitly assuming that the pulleys are solid cylinders with $I=\frac{1}{2}mr^2$]

One can see the cancellation in action. Consider a disk with moment of inertia $I = \frac{1}{2}m r^2$

Spin it up with tangential velocity $v$ so that its rotation rate is $\omega = \frac{v}{r}$.

Now its rotational energy is: $$\frac{1}{2}I \omega^2 = \frac{1}{2}(\frac{1}{2}mr^2)(\frac{v^2}{r^2}) = \frac{1}{4}mv^2$$which is independent of $r$ and is half the energy that the mass $m$ would have if it were moving velocity $v$.

 

[kuruman]

If set the zero of gravitational potential on m I have that:
$E_{initial}= E_{final}$ => $0= E_{m,gravitational} + E_{m,kinetic} + E_{1, kinetic} + E_{2,kinetic}$

=> $0= mgh + \frac 1 2 mv^2 + \frac 1 2 I_1ω_1 + \frac 1 2 I_2ω_2$. I don't know if there are any relationships between $ω_1$ and $ω_2$

How is the linear speed of the rim of a pulley related to the pulley's angular speed?

What is the value of $h$?

 

[Thermofox]

That doesn't look right. The radii and moments of inertia of the pulleys must be part of the answer. Please post your work.

$T_1 R_1= I_1 α_1$ => $T_1 R_1= \frac 1 2 M_1 R_1^2 \frac a {R_1}$ => $T_1 = \frac 1 2 M_1 a$

$(T_1 - T_2)R_2 = I_2 α_2$ => $(T_1 - T_2)R_2 = \frac 1 2 M_1 R_2^2 \frac a {R_2}$ => $T_2 = \frac 1 2 (M_1 + M_2)a$

I then substituted $T_2$ in $T_2 - mg = ma$ and found $a$.

 

[kuruman]

It is right. The radii of the pulleys is irrelevant. Only their masses matter.

It would be right if the pulleys are to be treated as solid cylinders. I edited my post to reflect that. I would correct your statement to say that only the effective masses $m_{\text{eff}}=I/R^2$ matter.

 

[Thermofox]

How is the linear speed of the rim of a pulley related to the pulley's angular speed?

What is the value of $h$?

$v_{rim} =ωR$ ?
$h = 2 ( 2 π R_1)$?

 

[kuruman]

This equation
$0= mgh + \frac 1 2 mv^2 + \frac 1 2 I_1ω_1 + \frac 1 2 I_2ω_2$
is incorrect. Check the rotational energies.

 

[Thermofox]

This equation
$0= mgh + \frac 1 2 mv^2 + \frac 1 2 I_1ω_1 + \frac 1 2 I_2ω_2$
is incorrect. Check the rotational energies.

Yeah you're right, I totally forgot to square them

 

[kuruman]

$v_{rim} =ωR$ ?
$h = 2 ( 2 π R_1)$?

Yes. No, see post #18.

 

[Thermofox]

Yes.

Oh wow, I guess I need to believe more in myself..... Thanks!

 

[kuruman]

Oh wow, I guess I need to believe more in myself..... Thanks!

Actually I made a mistake when I said "yes" in post #16. The problem says "Find the velocity of the block when Pulley 2 completes 2 full revolutions" so $R_1$ should be replaced with $R_2$. Sorry for the confusion. You should still believe in yourself, though.

 

[Thermofox]

Actually I made a mistake when I said "yes" in post #16. The problem says "Find the velocity of the block when Pulley 2 completes 2 full revolutions" so $R_1$ should be replaced with $R_2$. Sorry for the confusion. You should still believe in yourself, though.

Funnily enough I copied the text wrongly. The problem says 2 revolutions of the first pulley not the second as I had written. So yeah, I take the occasions to thank you again, thanks!