- #1
rudransh verma
Gold Member
- 1,067
- 96
- Homework Statement
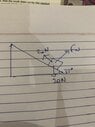
- A block of mass 2.0 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. (a) Show that the work done by the applied force does not exceed 40 J. (b) Find the work done by the force of gravity in that one second if the work done by the applied force is 40 J. (c) Find the kinetic energy of the block at the instant the force ceases
to act. Take g = 10 m/s
- Relevant Equations
- ##v=u+at##
##W=F.d##
##v^2=u^2+2as##
a) $$v=u+at$$
$$v=0+(F/m)t$$
$$v=-10$$
Now $$v^2=0+2as$$
$$s=-5$$
$$W=F.d=(-20)(-5)=100J>40$$
b) $$W=-mgh$$
$$W=-20(3)$$
$$W=-60$$
$$v=0+(F/m)t$$
$$v=-10$$
Now $$v^2=0+2as$$
$$s=-5$$
$$W=F.d=(-20)(-5)=100J>40$$
b) $$W=-mgh$$
$$W=-20(3)$$
$$W=-60$$