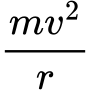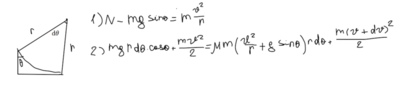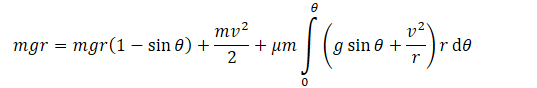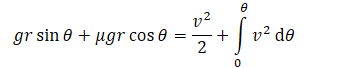zuzelle
- 6
- 1
- Homework Statement
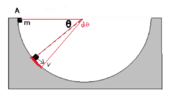
- A block of mass m rests at point A on a circular track of radius r with coefficient of friction u. It is then released with no initial speed. Find the dependance of velocity on angle, v(theta).
- Relevant Equations
- Potential Energy = mgh
Kinetic Energy = mv^2/2
Work done by a force = F*S
Centripetal force = mv^2/R
Since the friction is constantly changing because of both angle change and velocity change, I took a very small angle dθ, so that while the block is covering it, its velocity would change by dv, its height by rdθ*cosθ and the friction force wouldn't change much, because N isn't changing either.
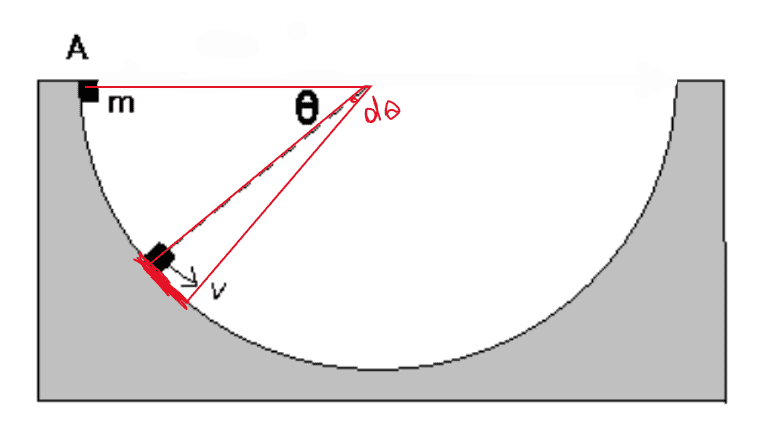
Then, I wrote the equation for centripetal force:
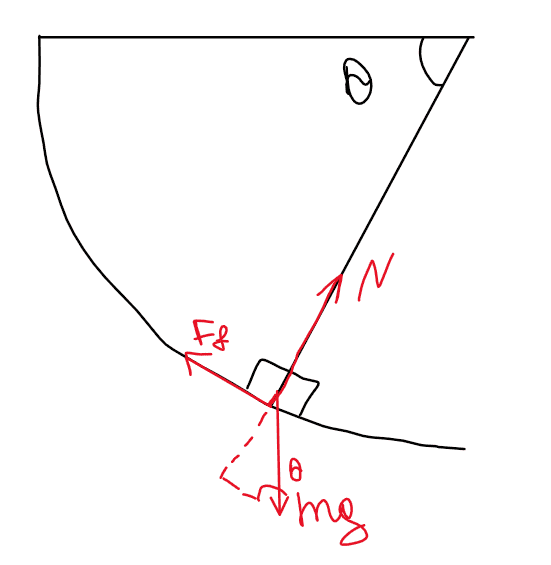
N - mgsin(θ) =
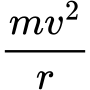
FBD:
Next, I thought of writing conservation of energy for this small displacement:
Potential energy + Kinetic energy = Work by friction on this small displacement + Kinetic Energy after.
So I got this:
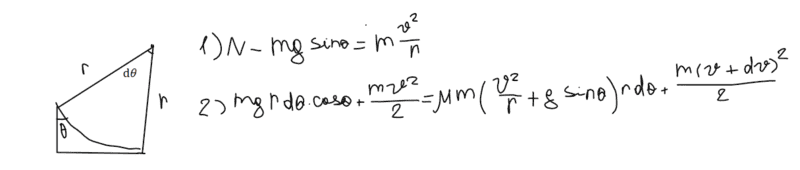
And I am not sure if this is right, because I end up getting an equation with differentials left, and it doesn't make sense. Could someone help, please?
Then, I wrote the equation for centripetal force:
N - mgsin(θ) =
FBD:
Next, I thought of writing conservation of energy for this small displacement:
Potential energy + Kinetic energy = Work by friction on this small displacement + Kinetic Energy after.
So I got this:
And I am not sure if this is right, because I end up getting an equation with differentials left, and it doesn't make sense. Could someone help, please?
Attachments
Last edited: