- #1
- 15,738
- 8,937
- Homework Statement
- A small block of mass ##m## is sliding on the inside of a vertical circular track of radius R. The coefficient of kinetic friction between the block and the track is μ. The block starts at the 9 o'clock position (point A) with speed ##v_0## and reaches the 3 o'clock position (point B) along two separate paths: (a) clockwise (top semicircle) or (b) counterclockwise (bottom semicircle). Assume that initial speed is high enough to keep the block in contact ith the track at all times. Gravity acts conventionally from top (12 o'clock) to bottom (6 o'clock).
Find the final speed at point B of the mass along the to paths.
- Relevant Equations
- ##F_{net} = ma.##
This problem is a reformulation and solution of a problem posted earlier that did not go very far. A streamlined solution is posted here for future reference.
The original post had an error which has now been fixed and the solution is, once more streamlined. See posts #4 and #5 for the historical background.
Solution
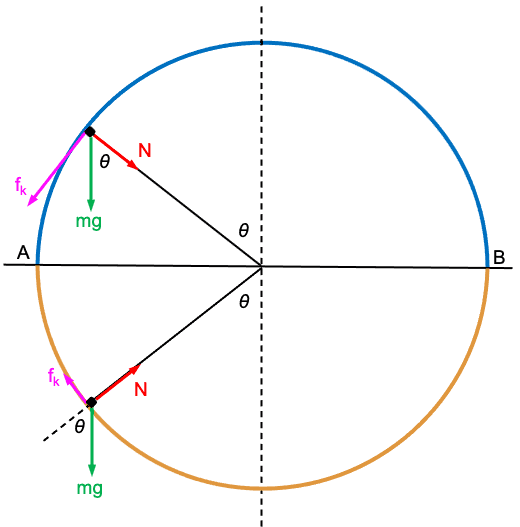Shown on the right are two FBDs for the two paths.
From the top FBD,
##N+mg\cos\theta=m\omega^2 R\implies N=m\omega^2 R-mg\cos\theta##
From the bottom FBD,
##N-mg\cos\theta=m\omega^2 R\implies N=m\omega^2 R+mg\cos\theta##
We combine the two into a single equation and write
##N=m\omega^2 R\mp mg\cos\theta.##
The force of friction for the two cases is
##f_k=\mu N=\mu m(\omega^2 R\mp g\cos\theta).##
The top/bottom sign corresponds to the top/bottom FBD. Before writing the tangential acceleration, we note that, in each case, ##~-\frac{\pi}{2}\leq \theta \leq \frac{\pi}{2}## Since the particle starts at A and ends at B in each case, ##\sin\theta## is negative in quadrants II (top FBD) and quadrant III (bottom FBD). The positive direction in each case is the direction of the linear velocity. Thus, the linear acceleration is
Top FBD:##~a_{\text{top}}=-\dfrac{f_k}{m}+g\sin\theta##
Bottom FBD:##~a_{\text{bot}}=-\dfrac{f_k}{m}-g\sin\theta##
The tangential acceleration for two cases combined is $$a_t=-\mu\omega^2 R \pm g(\sin\theta+ \mu\cos\theta).$$ Now $$a_t= R\frac{d\omega}{dt}=R\frac{d\omega}{d\theta}\frac{d\theta}{dt}=\omega R\frac{d\omega}{d\theta}.$$This results in the differential equation $$\omega \frac{d\omega}{d\theta}=-\mu\omega^2 \pm \frac{g}{R}(\sin\theta+\mu\cos\theta)$$ which we have to solve in order to answer the question. In the absence of gravity (##g=0##), the equation becomes ##~\dfrac{d\omega}{d\theta}=-\mu\omega~## which has solution ##\omega = Ce^{-\mu~\theta}.## This motivates trying a solution $$\omega(\theta)=f(\theta)e^{-\mu~\theta}.$$ The left-hand side is $$LHS=\omega \frac{d\omega}{d\theta}=fe^{-\mu~\theta}\left(\frac{df}{d\theta}e^{-\mu~\theta}-\mu fe^{-\mu~\theta}\right)=f\frac{df}{d\theta}e^{-2\mu~\theta}-\mu\omega^2.$$ Setting this equal to the RHS and canceling what cancels yields a separable equation, $$f\frac{df}{d\theta}=\pm \frac{g}{R}(\sin\theta+ \mu\cos\theta)e^{2\mu~\theta} \implies f~df=\pm g(\sin\theta+\mu\cos\theta)e^{2\mu~\theta}d\theta.$$ Using Wolfram Alpha for the integral on the RHS, we obtain $$
\begin{align} & \frac{1}{2}\left(f^2-f_0^2\right)=\pm\frac{g}{R}\frac{\left[(2\mu^2-1)\cos\theta+3\mu\sin\theta \right]}{[(4\mu^2+1)}{e^{2\mu \theta}} \nonumber \\
& f=\left\{f_0^2 \pm\frac{2g}{R}\frac{\left[(2\mu^2-1)\cos\theta+3\mu\sin\theta \right]}{(4\mu^2+1)}{e^{2\mu \theta}} \right\}^{1/2} \nonumber \\
& \implies \omega=\left\{f_0^2 \pm\frac{2g}{R}\frac{\left[(2\mu^2-1)\cos\theta+3\mu\sin\theta \right]}{(4\mu^2+1)}{e^{2\mu \theta}} \right\}^{1/2}e^{-\mu~\theta} \nonumber \\
\end{align}$$ The initial condition is ##\omega(-\pi/2)=v_0/R## and can be used to find ##f_0##. $$ \begin{align}
& \frac{v_0}{R}=\left [ f_0^2 \pm\frac{2g}{R}\frac{(-3)\mu}{(4\mu^2+1)}{e^{-\mu \pi}} \right]^{1/2}e^{\mu \pi/2}. \nonumber \\
& f_0^2=\left[ \frac{v_0^2}{R^2}\pm \frac{6\mu g}{(4\mu^2+1)R}\right]e^{-\mu \pi}. \nonumber \\
\end{align}$$ Finally, $$\omega= \left \{\left[ \frac{v_0^2}{R^2}\pm \frac{6\mu g}{(4\mu^2+1)R}\right]e^{-\mu( \pi+2\theta)} \pm\frac{2g}{R}\frac{\left[(2\mu^2-1)\cos\theta+3\mu\sin\theta \right]}{(4\mu^2+1)} \right\}^{1/2}.$$ At last we are in a position to find the speed at point B. $$\begin{align}
&\omega_B=\omega(\pi/2)= \left \{\left[ \frac{v_0^2}{R^2}\pm \frac{6\mu g}{(4\mu^2+1)R}\right]e^{-2\mu\pi} \pm\frac{6\mu g}{(4\mu^2+1)R} \right\}^{1/2}. \nonumber \\
& \omega_B= \left[\frac{v_0^2}{R^2}e^{-2\mu\pi}\pm\frac{6\mu g}{(4\mu^2+1)R}(1+e^{-2\mu\pi}) \right]^{1/2}\nonumber \\
& \implies v_B=\left[ v_0^2e^{-2\mu\pi}\pm \frac{6\mu gR}{(4\mu^2+1)}(1+e^{-2\mu\pi})\right]^{1/2} . \nonumber \\
\end{align}$$
The original post had an error which has now been fixed and the solution is, once more streamlined. See posts #4 and #5 for the historical background.
Solution
From the top FBD,
##N+mg\cos\theta=m\omega^2 R\implies N=m\omega^2 R-mg\cos\theta##
From the bottom FBD,
##N-mg\cos\theta=m\omega^2 R\implies N=m\omega^2 R+mg\cos\theta##
We combine the two into a single equation and write
##N=m\omega^2 R\mp mg\cos\theta.##
The force of friction for the two cases is
##f_k=\mu N=\mu m(\omega^2 R\mp g\cos\theta).##
The top/bottom sign corresponds to the top/bottom FBD. Before writing the tangential acceleration, we note that, in each case, ##~-\frac{\pi}{2}\leq \theta \leq \frac{\pi}{2}## Since the particle starts at A and ends at B in each case, ##\sin\theta## is negative in quadrants II (top FBD) and quadrant III (bottom FBD). The positive direction in each case is the direction of the linear velocity. Thus, the linear acceleration is
Top FBD:##~a_{\text{top}}=-\dfrac{f_k}{m}+g\sin\theta##
Bottom FBD:##~a_{\text{bot}}=-\dfrac{f_k}{m}-g\sin\theta##
The tangential acceleration for two cases combined is $$a_t=-\mu\omega^2 R \pm g(\sin\theta+ \mu\cos\theta).$$ Now $$a_t= R\frac{d\omega}{dt}=R\frac{d\omega}{d\theta}\frac{d\theta}{dt}=\omega R\frac{d\omega}{d\theta}.$$This results in the differential equation $$\omega \frac{d\omega}{d\theta}=-\mu\omega^2 \pm \frac{g}{R}(\sin\theta+\mu\cos\theta)$$ which we have to solve in order to answer the question. In the absence of gravity (##g=0##), the equation becomes ##~\dfrac{d\omega}{d\theta}=-\mu\omega~## which has solution ##\omega = Ce^{-\mu~\theta}.## This motivates trying a solution $$\omega(\theta)=f(\theta)e^{-\mu~\theta}.$$ The left-hand side is $$LHS=\omega \frac{d\omega}{d\theta}=fe^{-\mu~\theta}\left(\frac{df}{d\theta}e^{-\mu~\theta}-\mu fe^{-\mu~\theta}\right)=f\frac{df}{d\theta}e^{-2\mu~\theta}-\mu\omega^2.$$ Setting this equal to the RHS and canceling what cancels yields a separable equation, $$f\frac{df}{d\theta}=\pm \frac{g}{R}(\sin\theta+ \mu\cos\theta)e^{2\mu~\theta} \implies f~df=\pm g(\sin\theta+\mu\cos\theta)e^{2\mu~\theta}d\theta.$$ Using Wolfram Alpha for the integral on the RHS, we obtain $$
\begin{align} & \frac{1}{2}\left(f^2-f_0^2\right)=\pm\frac{g}{R}\frac{\left[(2\mu^2-1)\cos\theta+3\mu\sin\theta \right]}{[(4\mu^2+1)}{e^{2\mu \theta}} \nonumber \\
& f=\left\{f_0^2 \pm\frac{2g}{R}\frac{\left[(2\mu^2-1)\cos\theta+3\mu\sin\theta \right]}{(4\mu^2+1)}{e^{2\mu \theta}} \right\}^{1/2} \nonumber \\
& \implies \omega=\left\{f_0^2 \pm\frac{2g}{R}\frac{\left[(2\mu^2-1)\cos\theta+3\mu\sin\theta \right]}{(4\mu^2+1)}{e^{2\mu \theta}} \right\}^{1/2}e^{-\mu~\theta} \nonumber \\
\end{align}$$ The initial condition is ##\omega(-\pi/2)=v_0/R## and can be used to find ##f_0##. $$ \begin{align}
& \frac{v_0}{R}=\left [ f_0^2 \pm\frac{2g}{R}\frac{(-3)\mu}{(4\mu^2+1)}{e^{-\mu \pi}} \right]^{1/2}e^{\mu \pi/2}. \nonumber \\
& f_0^2=\left[ \frac{v_0^2}{R^2}\pm \frac{6\mu g}{(4\mu^2+1)R}\right]e^{-\mu \pi}. \nonumber \\
\end{align}$$ Finally, $$\omega= \left \{\left[ \frac{v_0^2}{R^2}\pm \frac{6\mu g}{(4\mu^2+1)R}\right]e^{-\mu( \pi+2\theta)} \pm\frac{2g}{R}\frac{\left[(2\mu^2-1)\cos\theta+3\mu\sin\theta \right]}{(4\mu^2+1)} \right\}^{1/2}.$$ At last we are in a position to find the speed at point B. $$\begin{align}
&\omega_B=\omega(\pi/2)= \left \{\left[ \frac{v_0^2}{R^2}\pm \frac{6\mu g}{(4\mu^2+1)R}\right]e^{-2\mu\pi} \pm\frac{6\mu g}{(4\mu^2+1)R} \right\}^{1/2}. \nonumber \\
& \omega_B= \left[\frac{v_0^2}{R^2}e^{-2\mu\pi}\pm\frac{6\mu g}{(4\mu^2+1)R}(1+e^{-2\mu\pi}) \right]^{1/2}\nonumber \\
& \implies v_B=\left[ v_0^2e^{-2\mu\pi}\pm \frac{6\mu gR}{(4\mu^2+1)}(1+e^{-2\mu\pi})\right]^{1/2} . \nonumber \\
\end{align}$$
Last edited:
owever, if positive ##r## grows outwards and positive ##\theta## grows counterclockwise, then it'd have a minus sign. Also, I'm having trouble to see how ##N## and ##mg\cos\theta## could be positive as well. They point inwards making ##r## smaller so it feels like they'd be negative. Similar to how in a xy coordinate system, a left-pointing force is negative when it accelerates the body in the negative direction.
