Block tied to a fixed string on an accelerating wedge

[Null_Void]

Homework Statement

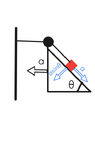
We have a block on a wedge, connected to a string which is fixed on a vertical wall to the left of the wedge.The string is horizontal and taut.
The wedge has an acceleration a towards the right. Mass of block is m.

Find the acceleration of the block
i) Relative to the ground
ii) Relative to the block

There is no friction anywhere.

Relevant Equations

Acceleration a along the incline

T - mg = ma

Acceleration along the normal to the incline

mgcosø - N = masinø

So I basically identified two constraints,

1) The string cannot be slack, therefore the acceleration of block down the incline should be equal to the acceleration of the wedge.

2) The block must always stay in contact with the wedge. Hence, the acceleration of the block normal to incline must be equal to the component of the wedge's acceleration along that directi
on.

The answer is given as option A which is absolutely not what I'm getting.
Also Acceleration of block w.r.t ground is given as 2aSinα/2, which is option (B) multiplied by a factor of 2; how did this come about?

So what what am I missing here ?
Is there anything wrong with my inference?


Here is a picture of the question,

 

[Orodruin]

(A) is essentially your first constraint …

 

[haruspex]

The answer is given as option A and B

But it says only one is correct?

 

[Null_Void]

(A) is essentially your first constraint …

I know relative motion is involved here, but I cannot understand how? Could you elaborate on how you came to that conclusion?
I thought that the acceleration of block along the incline will be 'a' in the ground frame. What am I missing here?

 

[Null_Void]

But it says only one is correct?

I'm sorry, I should have been more careful. I mistook option (B) to be multiplied by factor of 2, which is an answer given in the solution.
My Sincere Apologies for the mistake.

 

[kuruman]

I'm sorry, I should have clarified. Even though it says only one option is correct, both A and B are actually the correct answers. That's how it's given in the answer key

How can (A) be correct? If the acceleration of $m$ with respect to $M$ is $a$, then the velocity of $m$ will change in a different manner from the velocity of $M$ and the two masses will separate or fuse together. It looks like the answer key is incorrect or did I miss something?

 

[Null_Void]

How can (A) be correct? If the acceleration of $m$ with respect to $M$ is $a$, then the velocity of $m$ will change in a different manner from the velocity of $M$ and the two masses will separate or fuse together. It looks like the answer key is incorrect or did I miss something?

Here is the given solution :

I do not understand the solution at all as I'm still a bit confused about relative motion in such problems.

Any insight into analysing such situations is deeply appreciated

 

[Steve4Physics]

How can (A) be correct? If the acceleration of $m$ with respect to $M$ is $a$, then the velocity of $m$ will change in a different manner from the velocity of $M$ and the two masses will separate or fuse together. It looks like the answer key is incorrect or did I miss something?

I think the original question is badly written. References to ‘acceleration’ are really references to the magnitude of acceleration. The symbol ‘a’ should really be ‘|a|’.

The string has a horizontal part (length $p$) and a sloping part (length $q$). $\Delta p = -\Delta q$. It follows that $\frac {dp}{dt} = - \frac {dq}{dt}$ and $\frac {d^2p}{dt^2} = - \frac {d^2q}{dt^2}$.

The magnitude of the wedge’s acceleration relative to the ground is $|\frac {d^2p}{dt^2}|$.
The magnitude of the block’s acceleration relative to the wedge is $|\frac {d^2q}{dt^2}|$.
So these 2 magnitudes are equal (answer A).

 

[kuruman]

In my book "displacement" and "acceleration" are vectors; they have magnitude and direction. This question uses the terms rather carelessly and considers only the magnitude, which is what I missed. Choice (A) would be unamiguously True if it said "The magnitude of the acceleration of $m$ relative to $M$ is equal to the magnitude $a$."

That said, there is a simple way to get a handle on this. Note that if the wedge $M$ moves to the left by distance $d$, the piece to the left of the pulley is shortened by $d$ which means that mass $m$ moves down the incline also by distance $d$. The figure on the right shows the initial and final positions of mass $m$ at points A and B respectively.

Hint (on edit): In the accelerating frame of the wedge, the block travels distance $d$ under constant acceleration of magnitude $a$ in time $T$. In the inertial frame of the ground, the block travels distance AB under constant acceleration of magnitude $a_G$ also in time $T$. Some trigonometry is needed.

I think the original question is badly written. References to ‘acceleration’ are really references to the magnitude of acceleration.

I completely agree. The solution was informative.

 

[Null_Void]

I think the original question is badly written. References to ‘acceleration’ are really references to the magnitude of acceleration. The symbol ‘a’ should really be ‘|a|’.

The string has a horizontal part (length $p$) and a sloping part (length $q$). $\Delta p = -\Delta q$. It follows that $\frac {dp}{dt} = - \frac {dq}{dt}$ and $\frac {d^2p}{dt^2} = - \frac {d^2q}{dt^2}$.

The magnitude of the wedge’s acceleration relative to the ground is $|\frac {d^2p}{dt^2}|$.
The magnitude of the block’s acceleration relative to the wedge is $|\frac {d^2q}{dt^2}|$.
So these 2 magnitudes are equal (answer A).

But this is where I'm confused. I understand that the acceleration of block along the incline should be a. I initially thought that this acceleration would be w.r.t ground. How did you conclude that it is in the frame of the wedge?

 

[Orodruin]

How can (A) be correct? If the acceleration of $m$ with respect to $M$ is $a$, then the velocity of $m$ will change in a different manner from the velocity of $M$ and the two masses will separate or fuse together. It looks like the answer key is incorrect or did I miss something?

You are missing something. (A) is about the acceleration of m in the frame of M, which is non-inertial. It is easy to see that this is the case (as long as m stays on the block) because whatever else happens, the string length becomes longer at a rate which accelerates at $a$. Therefore, m must be accelerating with $a$ in the accelerating frame in which M is at rest.

 

[Null_Void]

In my book "displacement" and "acceleration" are vectors; they have magnitude and direction. This question uses the terms rather carelessly and considers only the magnitude, which is what I missed. Choice (A) would be unamiguously True if it said "The magnitude of the acceleration of $m$ relative to $M$ is equal to the magnitude $a$."

View attachment 352103That said, there is a simple way to get a handle on this. Note that if the wedge $M$ moves to the left by distance $d$, the piece to the left of the pulley is shortened by $d$ which means that mass $m$ moves down the incline also by distance $d$. The figure on the right shows the initial and final positions of mass $m$ at points A and B respectively.

Hint (on edit): In the accelerating frame of the wedge, the block travels distance $d$ under constant acceleration of magnitude $a$ in time $T$. In the inertial frame of the ground, the block travels distance AB under constant acceleration of magnitude $a_G$ also in time $T$. Some trigonometry is needed.


I completely agree. The solution was informative.

So when I first tried to solve this question, this is the FBD i came up with :

I simply applied the constraints I already mentioned.

In the frame of the wedge, there would be a rightward pseudoforce on the block.

The component of this force normal to plane will balance the masinø shown in the diagram,
The component of this force parallel to the plane will get added with the existing acceleration a.

Thus,
Net acc normal to incline = 0
Net acc parallel to incline = a + acosø

I know this is wrong, I would be grateful if you could point out why I'm wrong and explain how to deal with such cases.

Thanks in advance!

 

[PeroK]

So when I first tried to solve this question, this is the FBD i came up with :

I simply applied the constraints I already mentioned.

In the frame of the wedge, there would be a rightward pseudoforce on the block.

The component of this force normal to plane will balance the masinø shown in the diagram,
The component of this force parallel to the plane will get added with the existing acceleration a.

Thus,
Net acc normal to incline = 0
Net acc parallel to incline = a + acosø

I know this is wrong, I would be grateful if you could point out why I'm wrong and explain how to deal with such cases.

Thanks in advance!

Because the wedge is accelerating, it's tricky to calculate the contact force between the block and the wedge. This should be an unknown in your FBD. You could use the observation about the fixed length of the string in order to calculate this contact normal force- eventually.

As has already been pointed out the constraint of the string is the fundamental factor. If the wedge moves a distance $d$ to the left, then the pulley moves by a distance $d$ to the left, releasing string of length $d$, so that the mass $m$ slides a distance $d$ down the block - and, as it's constrainted to remain on the block(*), this must be relative to the block.

The displacement of $m$ relative to the ground is the vector sum of $d$ horizontally left, plus $d$ at an angle $\pi - \theta$. You can see this by imaginging that the wedge moves first and then the mass moves relative to the wedge.

This gives a total displacement of $d(1 - \cos \theta, sin \theta)$ relative to the ground (with left and down being positive). The magnitude of this is $2d\sin \frac \theta 2$, as per the answer key.

Differentiating twice wrt time gives the same equations for acceleration. You can then use the acceleration in the ground frame to calculate the contact force and complete your FBD.

(*) this constraint may be worth thinking about!

 

[Orodruin]

So when I first tried to solve this question, this is the FBD i came up with :

I simply applied the constraints I already mentioned.

In the frame of the wedge, there would be a rightward pseudoforce on the block.

The component of this force normal to plane will balance the masinø shown in the diagram,
The component of this force parallel to the plane will get added with the existing acceleration a.

Thus,
Net acc normal to incline = 0
Net acc parallel to incline = a + acosø

I know this is wrong, I would be grateful if you could point out why I'm wrong and explain how to deal with such cases.

Thanks in advance!

Why do you think the acceleration to the block normal to the incline (in the ground frame I suppose) would be $a\sin\alpha$? It is not correct. In the frame of the wedge this acceleration is zero because otherwise the block would either enter the wedge or lose contact.

In the wedge frame, it should be clear (as I stated and @PeroK detailed further) that acceleration is parallel to the wedge and has magnitude $a$. The acceleration in the ground frame is the vector sum of that acceleration and the acceleration of the wedge, ie, an isosceles triangle with apex angle $\alpha$. Its magnitude $a’$, by elementary geometry, is therefore given by the cosine theorem:
$$
a’^2 = a^2 + a^2 - 2a^2 \cos(\alpha) = 2a^2[1-\cos(\alpha)]
$$
or, taking the square root,
$$
a’ = 2a\sin(\alpha/2).
$$
The direction of the acceleration relative to the ground makes an angle $\alpha/2$ to the vertical. All of this can be deduced from the geometric constraints only. No force analysis is necessary.

Edit: The above also explains OP's question regarding why the (magnitude of) acceleration relative to the ground is twice $a\sin(\alpha/2)$.

Edit 2: Fixed a factor of 2 in the angle to the vertical.

 

[PeroK]

The direction of the acceleration relative to the ground makes an angle $\alpha$ to the vertical. All of this can be deduced from the geometric constraints only. No force analysis is necessary.

In many problems, we start with the forces and calculate the acceleration from a FBD. In this problem, we are given the acceleration (by some unspecified external force). The OP is learning that a force analysis is not immediately possible in these cases - and that we have to calculate the forces (the required external force could also be calculated) from the given acceleration of the system.

I remember having to think about this carefully when I first solved these kinds of problem.

 

[Orodruin]

It should also be added, in the wedge frame, the direction of gravity+pseudo force due to the frame being accelerating makes an angle $\phi = \arctan(g/a)$ to the horizontal. Whenever this angle is smaller than $\alpha$, there will be a net force on the block away from the wedge and it will lose contact. The requirement for the above to apply is therefore $\tan\alpha < g/a$ or, equivalently, $a < g/\tan\alpha$. For larger accelerations $a$, the block and wedge will lose contact.

There will also be a point where the string cannot remain taut, but let's leave that for another discussion.

 

[Orodruin]

In many problems, we start with the forces and calculate the acceleration from a FBD. In this problem, we are given the acceleration (by some unspecified external force). The OP is learning that a force analysis is not immediately possible in these cases - and that we have to calculate the forces (the required external force could also be calculated) from the given acceleration of the system.

I remember having to think about this carefully when I first solved these kinds of problem.

Sure, it is possible to compute the forces involved, but it is not required to solve the given problem.

 

[Null_Void]

Why do you think the acceleration to the block normal to the incline (in the ground frame I suppose) would be asin⁡α? It is not correct. In the frame of the wedge this acceleration is zero because otherwise the block would either enter the wedge or lose contact.

I thought that,
Say the wedge moves a distance x to the left. Now for the block to stay in contact with the wedge it must move a distance xsinø in the direction normal to the plane.
Thus double differentiating w.r.t to time
You can say that the acceleration will be equal to asinø

Why is this inference wrong?

 

[Null_Void]

Because the wedge is accelerating, it's tricky to calculate the contact force between the block and the wedge. This should be an unknown in your FBD. You could use the observation about the fixed length of the string in order to calculate this contact normal force- eventually.

I considered an example where there was simply a block on an accelerating wedge,
There is only constraint for the block, it should stay in contact with the wedge.
In this case, say if the wedge has a horizontal acceleration A to the left,
Then the block must have an acceleration Asinø in the direction normal to the plane.


In the original question, does the string being connected to the block make a difference, why would this acceleration be an unknown in this case?

Also could you expand on this statement as to how it must be relative to the block?

"and, as it's constrained to remain on the block(*), this must be relative to the block."

has already been pointed out the constraint of the string is the fundamental factor. If the wedge moves a distance d to the left, then the pulley moves by a distance d to the left, releasing string of length d, so that the mass m slides a distance d down the block - and, as it's constrainted to remain on the block(*), this must be relative to the block.

The displacement of m relative to the ground is the vector sum of d horizontally left, plus d at an angle π−θ. You can see this by imaginging that the wedge moves first and then the mass moves relative to the wedge.

This gives a total displacement of d(1−cos⁡θ,sinθ) relative to the ground (with left and down being positive). The magnitude of this is 2dsin⁡θ2, as per the answer key.

Differentiating twice wrt time gives the same equations for acceleration. You can then use the acceleration in the ground frame to calculate the contact force and complete your FBD.

It makes sense when you calculate in terms of the distance travelled and then differentiate to get the acceleration.

But I feel like when you try to analyse the forces it gets a bit complicated with you trying to identify what causes what.
Is there any way to solve this using forces and force analysis?
I would be really grateful to you if can show me how?

 

[PeroK]

But I feel like when you try to analyse the forces it gets a bit complicated with you trying to identify what causes what.
Is there any way to solve this using forces and force analysis?
I would be really grateful to you if can show me how?

I thought I already explained that. This is a kinematic problem, where you are given the motion of the system. Even if that has to be partly deduced from the problem statement.

In this case, you could calculate the forces, except gravity, from the motion. You should recognise that and solve the problem accordingly. You shouldn't insist on a force based analysis. That's not the only tool you need.

 

[Orodruin]

I thought that,
Say the wedge moves a distance x to the left. Now for the block to stay in contact with the wedge it must move a distance xsinø in the direction normal to the plane.
Thus double differentiating w.r.t to time
You can say that the acceleration will be equal to asinø

Why is this inference wrong?

It is not wrong in the ground frame, it is wrong in the wedge frame, which is the frame where the acceleration parallel to the wedge is $a$. The acceleration normal to the wedge in the wedge frame is zero.

If you want to look at the ground frame, the acceleration component parallel to the wedge will not be $a$.

 

[Lnewqban]

I considered an example where there was simply a block on an accelerating wedge,
There is only constraint for the block, it should stay in contact with the wedge.
In this case, say if the wedge has a horizontal acceleration A to the left,
Then the block must have an acceleration Asinø in the direction normal to the plane.


In the original question, does the string being connected to the block make a difference, why would this acceleration be an unknown in this case?

Consider also two additional examples in which the angle of the slope reaches the extreme values of 0° and 90°, and still there is no friction anywhere.

The only function of the pulley is to change the direction of the movement of the string and mass m.

Which answer would be correct in those two cases?

 

[PeroK]

Consider also two additional examples in which the angle of the slope reaches the extreme values of 0° and 90°, and still there is no friction anywhere.

The extreme case of zero angle is a good idea. At 90 degrees, the mass cannot keep in contact with the wedge.

 

[Lnewqban]

At 90 degrees, the mass cannot keep in contact with the wedge.

The way I see it: Assuming small enough acceleration, the mass m and its string will follow the horizontal movement of the pulley, which axle is solid part of the moving wedge.

That could be another example for the OP to consider:
Acceleration of the wedge being so small that the whole dynamic situation could be simplified to a movement of almost constant velocities.
That would also make the forces approach less practical than a simpler geometrical approach.

 

[Steve4Physics]

But this is where I'm confused. I understand that the acceleration of block along the incline should be a. I initially thought that this acceleration would be w.r.t ground. How did you conclude that it is in the frame of the wedge?

You may already have cleared-up any confusion, but in case not (and since it's quite important)...

The xy coordinate system is fixed to the ground with the x-axis horizontal; observer O is at its origin.

The x’y’ coordinate system is fixed to the wedge (at the wheel’s pivot) with the x’-axis parallel to the slope; observer O’ is at its origin

Measurements of displacement, velocity and acceleration made by O (in terms of xy values) are said to be ‘relative to the ground’ because O is ‘fixed’ to the ground.

Measurements of displacement, velocity and acceleration made by O’ (in terms of x’y’ values) are said to be ‘relative to the wedge’ because O’ is ‘fixed’ to the wedge.

For example, if the wedge moves 1m left, the x-coordinate of the wedge has decreased by 1m. The displacement of the wedge relative to the ground (relative to O) is 1m left (say from, x=10m to x = 9m).

In this case, because the rope’s length is fixed, the block moves 1m along the slope. The displacement of the block relative to the wedge (relative to O’) is 1m downhill (say from x’=2m to x’=3m).

The two displacements (wedge-relative-to ground and block-relative-to-wedge) have equal magnitudes (although their directions are different). Similar reasoning applies to the magnitudes of the two velocities and the two accelerations.

 

[Orodruin]

Assuming small enough acceleration, the mass m and its string will follow the horizontal movement of the pulley,

This is incorrect. However small the acceleration, the block will separate from the wedge when the angle goes to pi/2.

 

[Lnewqban]

This is incorrect. However small the acceleration, the block will separate from the wedge when the angle goes to pi/2.

But the small block will still move downwards at the same rate that the big block moves horizontally in that case.
Nowhere in the original problem I can see a mention to the condition of permanent contact between both blocks.

Noting that no option other than A would work for the extreme cases of α=0 or α=π/2 may help @Null_Void be less "confused about relative motion in such problems."

 

[Orodruin]

But the small block will still move downwards at the same rate that the big block moves horizontally in that case.

This is not generally true.

 

[erobz]

Would it be good if the OP tried to develop the Newtons Second system of equations for fun (I know I'd like it )?

 

[Null_Void]

You may already have cleared-up any confusion, but in case not (and since it's quite important)...
View attachment 352135
The xy coordinate system is fixed to the ground with the x-axis horizontal; observer O is at its origin.

The x’y’ coordinate system is fixed to the wedge (at the wheel’s pivot) with the x’-axis parallel to the slope; observer O’ is at its origin

Measurements of displacement, velocity and acceleration made by O (in terms of xy values) are said to be ‘relative to the ground’ because O is ‘fixed’ to the ground.

Measurements of displacement, velocity and acceleration made by O’ (in terms of x’y’ values) are said to be ‘relative to the wedge’ because O’ is ‘fixed’ to the wedge.

For example, if the wedge moves 1m left, the x-coordinate of the wedge has decreased by 1m. The displacement of the wedge relative to the ground (relative to O) is 1m left (say from, x=10m to x = 9m).

In this case, because the rope’s length is fixed, the block moves 1m along the slope. The displacement of the block relative to the wedge (relative to O’) is 1m downhill (say from x’=2m to x’=3m).

The two displacements (wedge-relative-to ground and block-relative-to-wedge) have equal magnitudes (although their directions are different). Similar reasoning applies to the magnitudes of the two velocities and the two accelerations.

First of all, A HUGE Thank you to you and everyone in this thread.
Your way of reasoning with the coordinate axes instantly made sense and most of my confusion has been resolved.
I understand that this is what user @kuruman tried to convey, but it didn't strike me at first.
I just have only last doubt remaining.
Now when I calculate the net acceleration in the ground frame, Along the incline I get this:

Acc = a - acosø

What gives rise to the extra term acosø
(Sorry if I'm being too clingy!)

 

[PeroK]

Now when I calculate the net acceleration in the ground frame, Along the incline I get this:

Acc = a - acosø

What gives rise to the extra term acosø

It's your equation, so you'd better tell us how you got that equation and what it's supposed to mean.

The full equations have already been posted in post #13.

I'm struggling to see why there are still any questions.

 

[Null_Void]

It's your equation, so you'd better tell us how you got that equation and what it's supposed to mean.

The full equations have already been posted in post #13.

I'm struggling to see why there are still any questions.

I understand your approach using the displacement of the block. It makes total sense.

But from the perspective of forces ( which i obviously understand are not a great way to solve certain problems from your post),

It seems like since the wedge moves to the left with an acceleration a, the block too moves along to the left with the same acceleration.
One component results into acosø opposite to the direction of motion of the block along the plane.
While the other component keeps it in contact with the wedge.

Thus we have,
Acc parallel to incline = a - acosø
Acc normal to incline = asinø

From my previous understanding of such problems which did not involve strings but rather only systems of blocks and wedges,
I remembered that just because the wedge accelerates horizontally with some acceleration, it doesn't mean that the block is directly affected by the motion. ( Such as having an acceleration of the same magnitude in the same direction as the wedge in the ground frame).
But since that obviously Isn't the case here and while I once again acknowledge your advice with a whole heart, I'm simply curious as to why this happens. The string obviously changes things, I'm just trying to get a deeper understanding of how.

 

[PeroK]

The string obviously changes things, I'm just trying to get a deeper understanding of how.

I don't think anything deep is going on. If the wedge moves, then the block can't stay where it is. It must slide down the wedge. If you don't see that, then I guess you don't see it.

The force of gravity on the block is important, of course - that's why there is a limit on how quickly the wedge can accelerate.

 

[kuruman]

Because the wedge is accelerating, it's tricky to calculate the contact force between the block and the wedge.

Not if you first use kinematics to find the acceleration of the block in the inertial frame as done above. Assuming a coordinate system such that $\mathbf {\hat x}$ is down the incline and $\mathbf {\hat y}$ is perpendicular and away from the incline (see figure on the right.)

From the drawing,
$$\beta =(90^{\circ}-\alpha/2) \implies
\begin{cases}\cos\!\beta=\sin(\alpha/2) \\ \sin\!\beta=\cos(\alpha/2)
\end{cases}$$The acceleration of the block relative to the ground is $$\begin{align} & \mathbf a_{\text{bg}}= a_{\text{bg}}(\cos\!\beta~ \mathbf {\hat x}-\sin\!\beta~ \mathbf{\hat y})= 2a \cos(\alpha/2)\left[\sin(\alpha/2)~\mathbf {\hat x}-\cos(\alpha/2)~ \mathbf{\hat y}\right] \nonumber \\
& = a\left[\sin\!\alpha~\mathbf {\hat x}-(1+\cos\!\alpha)~\mathbf{\hat y}\right] \nonumber
\end{align}$$
The standard FBD of a block on an incline yields
$$\begin{align} & T=mg\sin\!\alpha+ma \sin\!\alpha \nonumber \\
& N=mg\cos\!\alpha-ma(1+\cos\!\alpha). \nonumber
\end{align}$$ This post has been edited. See posts #35 and #36.

I'm struggling to see why there are still any questions.

Assuming a fixed value of the incline angle $\alpha$, I can see the following question to be explored using the above equations.
As the acceleration $a$ is increased, which of the two occurrences below happens first and at what value of $a$?

1. The block is detached from the surface.
2. The string goes slack.

 

[Null_Void]

Not if you first use kinematics to find the acceleration of the block in the inertial frame as done above. Assuming a coordinate system such that $\mathbf {\hat x}$ is down the incline and $\mathbf {\hat y}$ is perpendicular and away from the incline,

The acceleration of the block relative to the wedge is $~\mathbf a_{\text{bw}}=2a\cos(\alpha/2)~\mathbf {\hat x}$

The acceleration of the wedge relative to the ground is $~\mathbf a_{\text{wg}}=-a\cos(\alpha)~\mathbf {\hat x}-a\sin(\alpha)~\mathbf {\hat y}$

The acceleration of the block relative to the ground is $$\mathbf a_{\text{bg}}=\mathbf a_{\text{bw}}+\mathbf a_{\text{wg}}=[2a\cos(\alpha/2)-a\cos(\alpha)]\mathbf {\hat x}-a\sin(\alpha)~\mathbf {\hat y}.$$The standard FBD of a block on an incline yields
$$\begin{align} & T=mg\sin(\alpha)+m[2a\cos(\alpha/2)-a\cos(\alpha)] \nonumber \\
& N=mg\cos(\alpha)-ma\sin(\alpha). \nonumber
\end{align}$$

Assuming a fixed value of the incline angle $\alpha$, I can see the following question to be explored using the above equations.
As the acceleration $a$ is increased, which of the two occurrences below happens first and at what value of $a$?

1. The block is detached from the surface.
2. The string goes slack.

I think you made a mistake. The acceleration of block w.r.t to ground is 2acosα/2.