Block with upward velocity tethered to a bottom block

[annamal]

If I shoot a block with mass m1 with initial velocity v, and the block m1 goes to the end of the string tethered to the bottom block with m2 without lifting it up, what is the force equation involved with the block with m1?

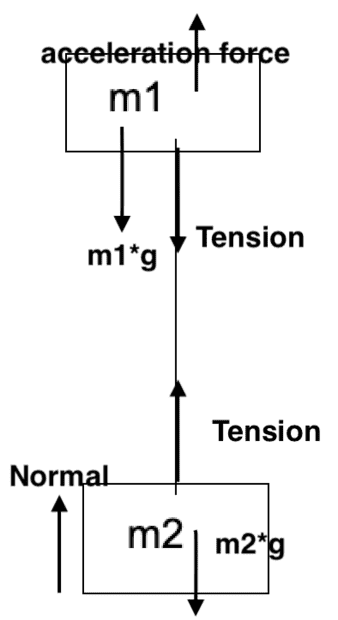
I am torn between whether it would be
1) -T -m1*g = 0, which I am unclear of because I thought the net acceleration would not be 0 and be -g
or this
2) -T = -m1*g, which would resolve that, but unsure if that is correct. Can someone verify it?

 

[erobz]

I don't think it's either of those. If block 2 isn't being lifted (accelerated) then I believe $T$ does not exceed $m_2g$

I think you want to think about Impluse/Momentum relationship here.

Imagine $m_1$ was a marble and $m_2$ was a fully loaded freight train. Tie the marble to a massless "super rope", that is basically a spring with a large $k$ value ( It has to have some ability to stretch, or we get some "infinities" I believe) and the other end to the freight train. Now just toss it up into the air and think about the magnitude of tension in the rope. Next, take that same marble tied to the "super rope", which it tied to the train and fire it out of a cannon. In which case do you suspect the tension in the rope to be higher? What is the difference between those two scenarios?

 

[nasu]

As long as the string is loose there is no tension. The only force on $m_1$ is the weight so the body $m_1$ moves as without the string, slowing down as it goes up. When it reaches the end of the string the tension increases up to a maximum value and during this interval you have a motion with variable acceleration. There may be a point where the tension is equal to the weight of $m_1$ (or not) but this is just for one single position in the upward motion. The body $m_1$ may stop before the tension becomes equal to $m_1g$. It may stop even before tension becomes non-zero. You don't have a relationship that is valid for any conditions and any point of the motion. It depends on the initial velocity, the length and stiffness of the string and the mass $m_1$ . But the tension and the weight are in the same direction so they should have the same sign even they don't have to be equal in magnitude. And the acceleration of $m_1$ is not zero.

 

[annamal]

As long as the string is loose there is no tension.

I am talking about the situation where there is tension and the velocity of the top block is enough to create a maximum tension but not enough to lift the bottom box. The string would be a limited length and the stiffness would be how stiff they are in normal string tension physics force problems.

I am also wondering how there would be a tension if the block only has an initial velocity and no acceleration.

The only force on $m_1$ is the weight so the body $m_1$ moves as without the string, slowing down as it goes up. When it reaches the end of the string the tension increases up to a maximum value and during this interval you have a motion with variable acceleration. There may be a point where the tension is equal to the weight of $m_1$ (or not) but this is just for one single position in the upward motion. The body $m_1$ may stop before the tension becomes equal to $m_1g$. It may stop even before tension becomes non-zero. You don't have a relationship that is valid for any conditions and any point of the motion. It depends on the initial velocity, the length and stiffness of the string and the mass $m_1$ . But the tension and the weight are in the same direction so they should have the same sign even they don't have to be equal in magnitude. And the acceleration of $m_1$ is not zero.

 

[Delta2]

Ha! I remember a problem like this was in an exams test in my second year of secondary high school (circa 1988-89)
But in that problem it was asking to find the final velocity of m_1 after the "collision" has take place, and by collision I mean the process that happens when the string becomes taut. It was solvable with conservation of momentum, making the assumption that the impulse of the weight of the two bodies is negligible in comparison to the impulse of the internal forces (the tensions). Here you want the (accurate) force equation which makes things a bit more complicated. Hold on if I can provide any useful insight on this.

 

[erobz]

If $m_2$ does not accelerate, we can basically model this as a mass $m_1$ tethered a light bungee cord of unstretched length $l_o$ which is tethered to the Earth. The cord is a spring. The linear spring is the idealization of a rope. After the height of the $m_1$ is $l_o$, assuming it still has some kinetic energy left the force of tension acting on $m_1$ is given by:

$x^+ \uparrow$

$$m_1 \ddot x = -T - m_1g$$

However, the tension is given by:

$$ T = kx $$

$$m_1 \ddot x = -kx - m_1g$$

You are going to have initial conditions that at $t = 0, x= 0$ and $v(0) = v_{l_o} = \sqrt{ v_g^2 - 2gl_o }$ where $v_g$ is the velocity the mass had at the ground.

You solve that second order ODE for $x(t)$ by normal methods, and then you can determine the Tension as a function of time acting on $m_1$.

If you are only interested in the maximum tension then apply conservation of energy:

$$ \frac{1}{2}m_1 v_{l_o}^2 = m_1 g x + \frac{1}{2} k x^2 + \frac{1}{2}m_1 \left( \frac{dx}{dt} \right)^2 \implies \frac{dx}{dt} = \sqrt { {v_{l_o}}^2 - 2gx - \frac{k}{m_1}x^2 } $$

The tension in the "spring" will be largest when the deflection $x$ is largest ( i.e when the mass instantaneously comes to rest ).

$$ 0 = \sqrt { {v_{l_o}}^2 - 2gx_{max} - \frac{k}{m_1}x_{max}^2 } $$

Then $T_{max}$ will be given by:

$$ T_{max} = k x_{max} $$

 

[Delta2]

Yes I think you going to have to model T as some function of x(post #6 models it as T=-kx) , otherwise the problem has infinitely many solutions for the tension T. My exact thought on this
Applying impulse-momentum theorem for each body:
$$\int_0^{\Delta t} (T+m_1g)dt=m_1v_1$$
$$\int_0^{\Delta t}(T+N-m_2g)dt=0$$

This system of two integral equations with two unknowns the tension T and the normal force N to the body $m_2$ on the ground has infinitely many solutions for any $\Delta t$.

 

[annamal]

If $m_2$ does not accelerate, we can basically model this as a mass $m_1$ tethered a light bungee cord of unstretched length $l_o$ which is tethered to the Earth. The cord is a spring. The linear spring is the idealization of a rope. After the height of the $m_1$ is $l_o$, assuming it still has some kinetic energy left the force of tension acting on $m_1$ is given by:

$x^+ \uparrow$

$$m_1 \ddot x = -T - mg$$

should $\ddot x$ = 0 since $m_1$ is not moving therefore should not have an acceleration?

However, the tension is given by:

$$ T = kx $$

$$m_1 \ddot x = -kx - mg$$

You are going to have initial conditions that at $t = 0, x= 0$ and $v(0) = v_o = \sqrt{ v_g^2 - 2gl_o }$ where $v_g$ is the velocity the mass had at the ground.

You solve that second order ODE for $x(t)$ by normal methods, and then you can determine the Tension as a function of time acting on $m_1$.

 

[jbriggs444]

end of the string

String or spring? Please be clear.

 

[annamal]

String or spring? Please be clear.

String but they are modeling it as a spring

 

[erobz]

String but they are modeling it as a spring

If you model it as something that is "inextensible" ( what I think you are trying to do) you run into some issues with infinite accelerations or it simply snapping. Pick your poison.

 

[Delta2]

Yes the tension must become infinite if you want the m1 to stop in zero time with zero displacement.

 

[erobz]

should $\ddot x = 0$ since $m_1$ is not moving therefore should not have an acceleration?

Are you implying that you want $m_1$ to instantaneously stop when it reaches a height $l_o$? Because $\ddot x = 0$ is completely the opposite of that. It would never stop if $\ddot x = 0$.

 

[annamal]

Are you implying that you want $m_1$ to instantaneously stop when it reaches a height $l_o$?

I am wondering does it instantaneously stop?

 

[erobz]

I am wondering does it instantaneously stop?

No, not in any real sense. If you wanted it to instantaneously stop that is going to result in an infinite force developing in the string. Do you think that is reasonable?

I personally feel that it is much more reasonable to say that everything is actually a bit of a spring to some extent with a finite $k$ value.

 

[annamal]

No, not in any real sense. If you wanted it to instantaneously stop that is going to result in an infinite force developing in the string. Do you thank that is reasonable?

I personally feel that it is much more reasonable to say that everything is actually a bit of a spring to some extent with a finite $k$ value.

Do you mean $m_1 \ddot x = -T - m_1g$, $m_1$ for the second m_1?

 

[erobz]

Do you $m_1 \ddot x = -T - m_1g$, $m_1$ for the second m_1?

It isn't clear what you are asking here?

 

[annamal]

It isn't clear what you are asking here?

I meant do you mean m_1 for the second m

 

[erobz]

I meant do you mean m_1 for the second m

I didn't see the typo. Fixed

 

[annamal]

Yes I think you going to have to model T as some function of x(post #6 models it as T=-kx) , otherwise the problem has infinitely many solutions for the tension T. My exact thought on this
Applying impulse-momentum theorem for each body:
$$\int_0^{\Delta t} (T+m_1g)dt=m_1v_1$$
$$\int_0^{\Delta t}(T+N-m_2g)dt=0$$

This system of two integral equations with two unknowns the tension T and the normal force N to the body $m_2$ on the ground has infinitely many solutions for any $\Delta t$.

Can you please explain how come there are infinitely many solutions for any $\Delta t$?

and can you explain why the tension has to become infinite in the below case?

Yes the tension must become infinite if you want the m1 to stop in zero time with zero displacement.

 

[Delta2]

Can you please explain how come there are infinitely many solutions for any $\Delta t$?

and can you explain why the tension has to become infinite in the below case?
"Yes the tension must become infinite if you want the m1 to stop in zero time with zero displacement."

Yes let's start from the last one which is easy. Right before the string becomes taut the body m1 has finite velocity let's call it $v_1$. Let's suppose that the solution to tension is given by $T(t)\Rightarrow a_1(t)=\frac{T(t)+m_1g}{m_1}=\frac{T(t)}{m_1}+g$ (t=0, right before the string becomes taut). If we want m1 to stop in finite time $\Delta t$ then the following equation must hold $$v_1=\int_0^{\Delta t} a_1 dt$$ (this equation is a direct implication of the definition of acceleration as the first derivative of velocity). Now if we take $\Delta t=0$ then the RHS of this equation becomes zero, hence it cannot hold (we assume $v_1\neq 0$), except in the case that the acceleration $a_1(t)$ is infinite in which case one might argue that the value of the integral becomes finite (though it will become a not well defined integral but anyway).

Now I ll give you two solutions for the tension (given a "collision" time $\Delta t>0$) and I think you ll get the idea how we can construct infinite solutions:
We can assume that tension is constant but finite during the collision time. Hence the first equation becomes $$T\Delta t+m_1g\Delta t=m_1v_1\Rightarrow T=\frac{m_1v_1}{\Delta t}-m_1g$$

Another assumption would be to assume that $T=kt$ for some constant k. Then the integral equation gives $$k\frac{(\Delta t)^2}{2}+m_1g\Delta t=m_1v_1\Rightarrow k=\frac{2m_1v_1}{(\Delta t)^2}-\frac{2m_1g}{\Delta t}$$ and for this value of k, the function $T=kt$ satisfies the first equation hence it is also a possible solution

Another assumption would be to set $T=k_1t+k_2t^2$. Working in similar way we can solve for $k_1$ and $k_2$ (one of them will be a free variable) and then the Tension for those $k_1$ and $k_2$ is also a solution. And so on i think you get the idea how we can have infinitely many solutions.

 

[Delta2]

The point is that those integral equations are very relaxed. The only thing they tell us, is that the body has to stop in finite time $\Delta t$. In how many ways you can stop a body of some initial velocity in some finite time. There are infinitely many ways.

 

[annamal]

Yes let's start from the last one which is easy. Right before the string becomes taut the body m1 has finite velocity let's call it $v_1$. Let's suppose that the solution to tension is given by $T(t)\Rightarrow a_1(t)=\frac{T(t)+m_1g}{m_1}=\frac{T(t)}{m_1}+g$ (t=0, right before the string becomes taut). If we want m1 to stop in finite time $\Delta t$ then the following equation must hold $$v_1=\int_0^{\Delta t} a_1 dt$$ (this equation is a direct implication of the definition of acceleration as the first derivative of velocity). Now if we take $\Delta t=0$ then the RHS of this equation becomes zero, hence it cannot hold (we assume $v_1\neq 0$), except in the case that the acceleration $a_1(t)$ is infinite in which case one might argue that the value of the integral becomes finite (though it will become a not well defined integral but anyway).

Now I ll give you two solutions for the tension (given a "collision" time $\Delta t>0$) and I think you ll get the idea how we can construct infinite solutions:
We can assume that tension is constant but finite during the collision time. Hence the first equation becomes $$T\Delta t+m_1g\Delta t=m_1v_1\Rightarrow T=\frac{m_1v_1}{\Delta t}-m_1g$$

Should the equations have a negative sign and be
$\int_0^{\Delta t} (-T-m_1g)dt=m_1v_1$?

Another assumption would be to assume that $T=kt$ for some constant k. Then the integral equation gives $$k\frac{(\Delta t)^2}{2}+m_1g\Delta t=m_1v_1\Rightarrow k=\frac{2m_1v_1}{(\Delta t)^2}-\frac{2m_1g}{\Delta t}$$ and for this value of k, the function $T=kt$ satisfies the first equation hence it is also a possible solution

Another assumption would be to set $T=k_1t+k_2t^2$. Working in similar way we can solve for $k_1$ and $k_2$ (one of them will be a free variable) and then the Tension for those $k_1$ and $k_2$ is also a solution. And so on i think you get the idea how we can have infinitely many solutions.

Ok, that makes sense

 

[Delta2]

Should the equations have a negative sign and be

You can put minuses there like that, but then the tension will be found negative (if we take $v_1$ as positive going up). Yes I guess you can do that if you want to encode into the minus sign the direction of tension with respect to the direction of v1.

 

[erobz]

Should the equations have a negative sign and be
$\int_0^{\Delta t} (-T-m_1g)dt=m_1v_1$?

Just so there is no confusion, @Delta2 is taking $v_1$ to the instantaneous velocity, not the initial velocity $v_{l_o}$.

So we have that:

$$ \vec{p_f} - \vec{p_o} = \int_0^{\Delta t} \vec{F} dt $$

$$ m_1\vec{ v_1} - m_1 \vec{ v_{l_o} } = \int \left( -T -m_1 g \right) dt $$

So that if we take the derivate of both sides with respect to time we get back to:

$$ \frac{d}{dt} \left( m_1\vec{ v_1} - m_1 \vec{ v_{l_o} } \right) = -T -m_1 g $$

$$ m_1 \ddot x_1 = -T -m_1 g $$

So whatever you do with the signs on the forces, just make sure you get back to the convention you assumed to write the equations.

 

[Delta2]

Just so there is no confusion, @Delta2 is taking $v_1$ to the instantaneous velocity, not the initial velocity $v_{l_o}$.

So we have that:

$$ \vec{p_f} - \vec{p_o} = \int_0^{\Delta t} \vec{F} dt $$

$$ m_1\vec{ v_1} - m_1 \vec{ v_{l_o} } = \int \left( -T -m_1 g \right) dt $$

So that if we take the derivate of both sides with respect to time we get back to:

$$ \frac{d}{dt} \left( m_1\vec{ v_1} - m_1 \vec{ v_{l_o} } \right) = -T -m_1 g $$

$$ m_1 \ddot x_1 = -T -m_1 g $$

So whatever you do with the signs on the forces, just make sure you get back to the convention you assumed to write the equations.

Nope I took $v_1=v(0)$ as the initial velocity and $v(\Delta t)=0$ the final velocity. I should have been more careful with the signs, The correct equation imo is $$\int_0^{\Delta t}(T+mg)dt=-m_1v_1$$ (assuming that T is pointing down like gravity).

 

[Delta2]

Someone can say that to model the force of a string as $T(t)=k_1t+k_2t^2$ is not a realistic model for the Tension of a string, and probably he is right, but I said before that we must model somehow the Tension, if we leave it there like any other force, then the problem has infinite solutions.

 

[erobz]

Nope I took $v_1=v(0)$ as the initial velocity and $v(\Delta t)=0$ the final velocity. I should have been more careful with the signs, The correct equation imo is $$\int_0^{\Delta t}(T+mg)dt=-m_1v_1$$ (assuming that T is pointing down like gravity).

Well, maybe the other way was correct. I can't see how that integral could be negative, maybe I'm not thinking clearly though. Sorry If I'm confusing you on this issue.

$x \uparrow^+$

$$ 0 -m_1v_1 = \int_0^{\Delta t}(-T-mg)dt$$

Implies what you had:

$$ m_1 v_1 = \int_0^{\Delta t}(T+mg)dt $$

I'm not sure which way is up anymore, let's skip these formalities and see if we can add some variable mass to this