Boats in a triangle colliding after some time

[RubroCP]

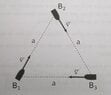
Assume that three boats, $B_1$, $B_2$ and $B_3$ travel on a lake with a constant magnitude velocity equal to $v$. $B_1$ always travels towards $B_2$, which in turn travels towards $B_3$ which ultimately travels towards $B_1$. Initially, the boats are at points on the water surface that form an equilateral triangle with an edge $a$, as shown in the following figure.

a) How long does it take for the boats to meet?

b) Calculate the expression of the trajectory described by one of the three boats.

GAB:
a) $t=\frac{2a}{3v}$
b) $r(\theta)=\frac{a\sqrt{3}}{3}e^{-\sqrt{3}\theta}$Hi guys, I would like some help in solving this problem. I first tried to describe the initial movement of each boat vectorly and tried to find the point where the boats collide. However, I've just noticed that the angle $\theta$ doesn't stay constant, so the velocity vector changes with each passing second. I've already solved a similar problem in Irodov, with turtles heading towards each other if I'm not mistaken, but the question didn't ask to describe the position as a function of time. I really appreciate it if you can help me with ideas.

 

[ergospherical]

Here is a hint. After a small time $\delta t$, then to first order in $\delta t$ each boat has moved $v\delta t$ along the edge of the triangle:

This results in a new equilateral triangle, of slightly shorter side length. What is the side length of this new triangle to first order in $\delta t$? What is the change $\delta l$ in side length in time $\delta t$? What is $\delta l / \delta t$?

(You can imagine drawing a sequence of smaller and smaller such triangles until the boats collide. )

 

[jbriggs444]

Much can be deduced as consequences of the symmetry of the problem.