guyvsdcsniper
- 264
- 37
- Homework Statement
- Give numerical values of ω that define the ranges where ω can be written as a power law and give the Bode-plot slope in each range, using decibels per dec or oct
- Relevant Equations
- db=log(v2/v1)
From 0 to ##10^3## ##\omega## there is a dB gain, from ##10^3## to ##10^5## there is another. Finally from ##10^5## to infinity the slope is constant (0).
I know the formula
$$dbV= 20log_{10}\frac{V_2}{V_1}$$
can give me the slope but that is in terms of Volts, but I have frequency and the magnitude of the transfer function. I cant find a formula in my book or online to calculate the dB gain with these two.
Is there an approach to determining the slope of each with the information given in the image?
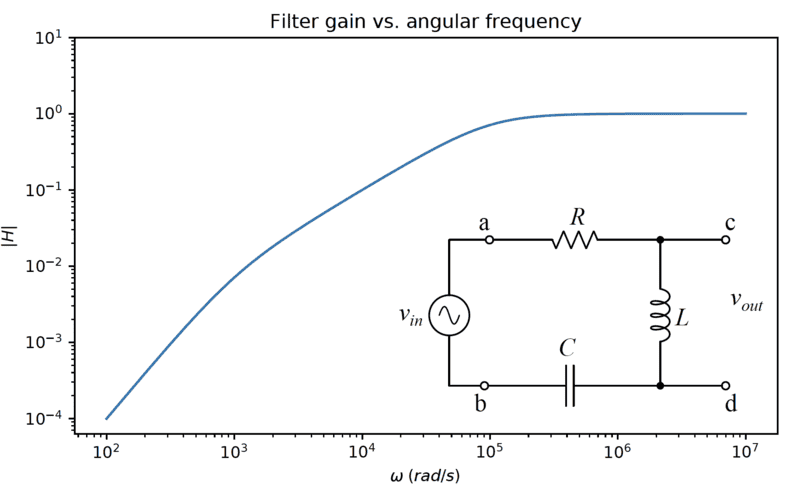
I know the formula
$$dbV= 20log_{10}\frac{V_2}{V_1}$$
can give me the slope but that is in terms of Volts, but I have frequency and the magnitude of the transfer function. I cant find a formula in my book or online to calculate the dB gain with these two.
Is there an approach to determining the slope of each with the information given in the image?