kekpillangok
- 15
- 2
- Homework Statement
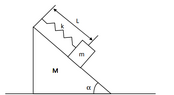
- A body of mass 𝑚 slides without friction on the flat surface (which is inclined at an angle 𝛼 relative to the horizontal) of a block of mass 𝑀 under the action of a spring, as shown in the figure. This spring, with a spring constant 𝑘 and a natural length 𝐶, has its ends fixed respectively to the body of mass 𝑚 and to the block. In turn, the block can slide without friction on the flat and horizontal surface on which it rests. The body is pulled up to a position where the spring is stretched to a length 𝐿 (𝐿 > 𝐶), such that, when released, the body passes through the position where the elastic force is zero. In this position, what is the magnitude of the velocity of the block in terms of L, C, m, M, g (acceleration of gravity), 𝛼, and k?
- Relevant Equations
- E_s = kx^2 / 2
Ek + Ep + E_s = K
I was taught to solve this problem by first finding the velocity of the body (of mass ##m ##) relative to the block of mass ##M ##. One way of doing this is as follows: first write $$ {v _{m _{B }}}^{2 }={v _{mx _{B }}}^{2 }+{v _{my }}^{2 } (I) $$
where ##{v _{m _{B }}} ## is the magnitude of the velocity of the body of mass ##m ## with respect to the block, and the other terms are the horizontal and vertical components of that velocity. Then, we know that $$v _{mx }=v _{mx _{B }}-v _{M } (II) $$
where ##v _{mx } ## is the horizontal component of the velocity of the body relative to the earth and ##v _{M } ## is the velocity of the block, also relative to the earth. ##v _{M } ## is what we want to find.
Also, because momentum is conserved, we have $$m \cdot v _{mx }=M \cdot v _{M } (III) $$.
Now, from equations II and III, we get ##v _{mx _{B }}=v _{M }{\left( \frac{M +m }{m }\right) } ##. Then, if we look at the geometry of the velocity of the body relative to the block, we see that ##\tan \left( \alpha \right) \, =\frac{v _{my }}{v _{mx _{B }}} ##. This lets you solve for the ## y ## component of the velocity of the body relative to the block in terms of the velocity of the block. Replacing these components into equation I and finally into the relationship for energy conservation—$$\frac{1 }{2 }k {{\left( L -C \right) }}^{2 }=\frac{1 }{2 }m {v _{m }}^{2 }+\frac{1 }{2 }M {v _{M }}^{2 }+m g {\left( L -C \right) }\sin \left( \alpha \right) \, $$
—lets you solve for ## v _{M }## in terms of the given parameters.
This way of solving the problem is clear to me. What I don't understand is, why can't I just find the magnitude of the velocity of the body relative to the block directly by writing $$ \frac{1 }{2 }k {{\left( L -C \right) }}^{2 }=\frac{1 }{2 }m {v _{m B }}^{2 }+m g {\left( L -C \right) }\sin \left( \alpha \right) \, $$
and solving for ##v _{mB } ##? Isn't it true that, relative to the block, all the elastic potential energy gets converted only into kinetic energy and gravitational potential energy for the body?
This would give me a value of ##\sqrt{\frac{k {{\left( L -C \right) }}^{2 }-2 m g {\left( L -C \right) }\sin \left( \alpha \right) \, }{m }}\cos \left( \alpha \right) \, ## for the horizontal component of the velocity of the body relative to the block. This value minus ## v _{M }## should equal the horizontal component of the velocity of the body relative to the earth, which could then be plugged into the conservation of momentum expression and so allow me to find ## v _{M }##. This approach, however, does not lead to the right answer. Why doesn't it work? I really can't see why energy doesn't get converted the way I expect it to.
The right answer, obtained by the first method, is ## v _{M }=\sqrt{\frac{2 m {\left[ \frac{1 }{2 }k {{\left( L -C \right) }}^{2 }-m g {\left( L -C \right) }\sin \left( \alpha \right) \, \right] }}{{\left( m +M \right) }{\left[ {\left( m +M \right) }\tan ^{2 } \left( \alpha \right) \, +M \right] }}}##.
The answer I arrived at by the second method, which was the idea I came up with first, was ##v _{M }=\sqrt{\frac{2 m {\left[ \frac{1 }{2 }k {{\left( L -C \right) }}^{2 }-m g {\left( L -C \right) }\sin \left( \alpha \right) \, \right] }}{{{\left( M +m \right) }}^{2 }{\left( 1 +\tan ^{2 } \alpha \, \right) }}} ##.
I know this is really messy, but any help will be greatly appreciated. My doubt, at any rate, is a simple one: why can't I find the velocity of the body relative to the block by "pretending" that all the energy gets converted into kinetic energy and g.p.e for the body?
where ##{v _{m _{B }}} ## is the magnitude of the velocity of the body of mass ##m ## with respect to the block, and the other terms are the horizontal and vertical components of that velocity. Then, we know that $$v _{mx }=v _{mx _{B }}-v _{M } (II) $$
where ##v _{mx } ## is the horizontal component of the velocity of the body relative to the earth and ##v _{M } ## is the velocity of the block, also relative to the earth. ##v _{M } ## is what we want to find.
Also, because momentum is conserved, we have $$m \cdot v _{mx }=M \cdot v _{M } (III) $$.
Now, from equations II and III, we get ##v _{mx _{B }}=v _{M }{\left( \frac{M +m }{m }\right) } ##. Then, if we look at the geometry of the velocity of the body relative to the block, we see that ##\tan \left( \alpha \right) \, =\frac{v _{my }}{v _{mx _{B }}} ##. This lets you solve for the ## y ## component of the velocity of the body relative to the block in terms of the velocity of the block. Replacing these components into equation I and finally into the relationship for energy conservation—$$\frac{1 }{2 }k {{\left( L -C \right) }}^{2 }=\frac{1 }{2 }m {v _{m }}^{2 }+\frac{1 }{2 }M {v _{M }}^{2 }+m g {\left( L -C \right) }\sin \left( \alpha \right) \, $$
—lets you solve for ## v _{M }## in terms of the given parameters.
This way of solving the problem is clear to me. What I don't understand is, why can't I just find the magnitude of the velocity of the body relative to the block directly by writing $$ \frac{1 }{2 }k {{\left( L -C \right) }}^{2 }=\frac{1 }{2 }m {v _{m B }}^{2 }+m g {\left( L -C \right) }\sin \left( \alpha \right) \, $$
and solving for ##v _{mB } ##? Isn't it true that, relative to the block, all the elastic potential energy gets converted only into kinetic energy and gravitational potential energy for the body?
This would give me a value of ##\sqrt{\frac{k {{\left( L -C \right) }}^{2 }-2 m g {\left( L -C \right) }\sin \left( \alpha \right) \, }{m }}\cos \left( \alpha \right) \, ## for the horizontal component of the velocity of the body relative to the block. This value minus ## v _{M }## should equal the horizontal component of the velocity of the body relative to the earth, which could then be plugged into the conservation of momentum expression and so allow me to find ## v _{M }##. This approach, however, does not lead to the right answer. Why doesn't it work? I really can't see why energy doesn't get converted the way I expect it to.
The right answer, obtained by the first method, is ## v _{M }=\sqrt{\frac{2 m {\left[ \frac{1 }{2 }k {{\left( L -C \right) }}^{2 }-m g {\left( L -C \right) }\sin \left( \alpha \right) \, \right] }}{{\left( m +M \right) }{\left[ {\left( m +M \right) }\tan ^{2 } \left( \alpha \right) \, +M \right] }}}##.
The answer I arrived at by the second method, which was the idea I came up with first, was ##v _{M }=\sqrt{\frac{2 m {\left[ \frac{1 }{2 }k {{\left( L -C \right) }}^{2 }-m g {\left( L -C \right) }\sin \left( \alpha \right) \, \right] }}{{{\left( M +m \right) }}^{2 }{\left( 1 +\tan ^{2 } \alpha \, \right) }}} ##.
I know this is really messy, but any help will be greatly appreciated. My doubt, at any rate, is a simple one: why can't I find the velocity of the body relative to the block by "pretending" that all the energy gets converted into kinetic energy and g.p.e for the body?