Body forces in static equilibrium (FEM issue)

[skrat]

TL;DR Summary

According to Zienkiewicz, the body forces in static equilibrium should equal zero, but in my simulations they don't.

Hi,

I have an issue with understanding the body forces in the context of FEM simulations. I am using freefem to do the simulations.

So I took a simple unit cube, fixed the displacements at side $x=0$ and prescribed a displacement $u_x = 0.025$ at $x=1$. If required, the entire script is given below.

[CODE title="Cube example"]load "medit"
include "cube.idp"
int[int] numberOfNodes = [4, 4, 4]; // Nodes per side.
real [int, int] boundaryRange = [[0.0, 1.0], [0.0, 1.0], [0.0, 1.0]]; // Side lengths.
int [int, int] labels = [[1, 2], [3, 4], [5, 6]]; // Labels.
mesh3 Th = Cube(numberOfNodes, boundaryRange, labels);

real E = 2230e6;
real sigma = 0.4;
real mu = E/(2*(1+sigma));
real lambda = E*sigma/((1+sigma)*(1-2*sigma));

fespace Vh(Th,P2);
Vh u1,u2,u3, v1,v2,v3;

real sqrt2=sqrt(2.);
macro epsilon(u1,u2,u3) [dx(u1),dy(u2),dz(u3),(dz(u2)+dy(u3))/sqrt2,(dz(u1)+dx(u3))/sqrt2,(dy(u1)+dx(u2))/sqrt2] // EOM
macro div(u1,u2,u3) ( dx(u1)+dy(u2)+dz(u3) ) // EOM

solve Lame([u1,u2,u3],[v1,v2,v3])=
int3d(Th)(
lambda*div(u1,u2,u3)*div(v1,v2,v3)
+2.*mu*( epsilon(u1,u2,u3)'*epsilon(v1,v2,v3) ) //')
)
// - int3d(Th) (gravity*v3)
+ on(1,u1=0,u2=0,u3=0)
+ on(2,u1=0.025)
;

real dmax = u3[].max;
cout << " max deplacement = " << dmax << endl;
real coef= 0.1/dmax;
int[int] ref2=[1,0,2,0];
mesh3 Thm=movemesh3(Th,transfo=[x+u1*coef,y+u2*coef,z+u3*coef],label=ref2);
Thm=change(Thm,label=ref2);
plot(Th,Thm, wait=1,cmm="coef amplification = "+coef );[/CODE]

Now the results look completely fine to me:

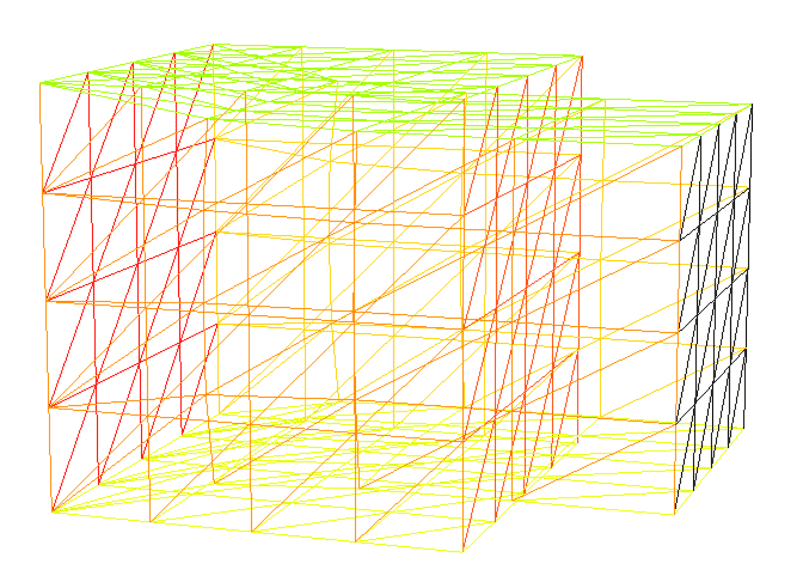
However, the problem.

The problems start when I try to compute the body forces. Now, according to O.C. Zienkiewicz, ... J.Z. Zhu, in The Finite Element Method: its Basis and Fundamentals (Seventh Edition), 2013 (snapshot of a chapter given here) for any element in the static equilibrium we can write
$$\nabla \cdot \sigma + b = 0$$
where $\sigma$ is the stress tensor and $b$ is a vector of body forces.

Now in my case, there are no external body forces (e.g. gravity), so $b=0$ which in turn means $\nabla \cdot \sigma = 0$.

So I computed the divergence of the stress tensor, where the divergence of a tensor $T$ is defined as

$$ (\nabla \cdot T)_i = \frac{\partial T_{ij}}{\partial x_j} $$

assuming the Einstein summation rule.

Here is my script:

[CODE title="Stress divergence computation."]// UPDATE
macro getTensorDivX(sxx, syy, szz, syz, sxz, sxy) (dx(sxx) + dy(sxy) + dz(sxz)) // EOM
macro getTensorDivY(sxx, syy, szz, syz, sxz, sxy) (dx(sxy) + dy(syy) + dz(syz)) // EOM
macro getTensorDivZ(sxx, syy, szz, syz, sxz, sxy) (dx(sxz) + dy(syz) + dz(szz)) // EOM
macro sigma(u1, u2, u3) [(lambda + 2 * mu) * dx(u1) + lambda * dy(u2) + lambda * dz(u3),
lambda * dx(u1) + (lambda + 2 * mu) * dy(u2) + lambda * dz(u3),
lambda + dx(u1) + lambda * dy(u2) + (lambda + 2 * mu) * dz(u3),
2 * mu * (dz(u2)+dy(u3)),
2 * mu * (dz(u1)+dx(u3)),
2 * mu * (dy(u1)+dx(u2))] // EOM

fespace Nh(Th, P1);
Nh sxx, syy, szz, syz, sxz, sxy;
Nh rx, ry, rz, r;

// Compute stresses.
sxx = sigma(u1, u2, u3)[0];
syy = sigma(u1, u2, u3)[1];
szz = sigma(u1, u2, u3)[2];
syz = sigma(u1, u2, u3)[3];
sxz = sigma(u1, u2, u3)[4];
sxy = sigma(u1, u2, u3)[5];

// Compute residuums.
rx = getTensorDivX(sxx, syy, szz, syz, sxz, sxy);
ry = getTensorDivY(sxx, syy, szz, syz, sxz, sxy);
rz = getTensorDivZ(sxx, syy, szz, syz, sxz, sxy);

for (int i = 0; i < r.n; i++) {
r[] = dist(rx[], ry[], rz[]);
}

cout << "Average body force (stress divergence) = " << r[].sum / r.n << endl;[/CODE]

But I was extremely surprised to find out that the average norm of body forces is of order $10^7$, which is not even close to 0.

Question

I have two questions.

1. I am not expecting that any of you is familiar with the FreeFem++. If you are, even better, you can help me understand what I am doing wrong in my script.
2. Am I making wrong assumptions? Should I not be surprised that the divergence of the stress tensor is not zero? Is this not even a problem but rather an expected result? If yes, could you help me understand why?

 

[pasmith]

I think the conclusion is that your medium is not in static equilibrium.

You are essentially pulling the medium along the x-axis in order to achieve the displacement. If you want the result to be in static equilibrium, you need to apply an external force to resist the medium's desire to return to its equilibrium (u \equiv 0) state.

I'm also not convinced that your definition of \sigma is consistent with your definition of \epsilon. Generally in a linear theory you would have <br /> \epsilon_{ij} = \frac12 \left( \frac{\partial u_i}{\partial x_j} +\frac{\partial u_j}{\partial x_i}\right) and <br /> \sigma_{ij} = 2\mu \epsilon_{ij} + \lambda \epsilon_{kk} \delta_{ij}.

 

[skrat]

Yes, you are correct, my definition of $\sigma$ is a wrong by factor 2 on all off-diagonal terms.

What if, excuse me for brainstorming, I wanted to take the last term from the weak formulation of the hookean law
$$ \int _\Omega \nabla\cdot \sigma v \mathrm{d} \Omega $$
and decided to play with a little. For example use the calculus identity
$$\nabla \cdot (\sigma v) = (\nabla \cdot \sigma)v + \sigma \nabla v.$$
This would allow me to rewrite the term to
$$ \int _\Omega \nabla\cdot \sigma v \mathrm{d} \Omega = \int _\Omega \sigma \nabla v \mathrm{d} \Omega + \int _\Omega \nabla\cdot (\sigma v) \mathrm{d} \Omega $$
and using the Divergence theorem the last integral can be over $\partial \Omega$ finally resulting in
$$ \int _\Omega \nabla\cdot \sigma v \mathrm{d} \Omega = \int _\Omega \sigma \nabla v \mathrm{d} \Omega+ \int _{\partial \Omega} \hat{n} \cdot \sigma v \mathrm{d} \partial \Omega.$$

I may be shooting blanks with this but the second interval could be zero as $v$ can always be set to 0 on the boundary $\partial \Omega$. If that is true than computing the first integral is all that remains.

Does that make any sense? Would this help at all? If nothing else it should improve the numerical stability where the cube is fixed as computation of derivatives of stress tensor components there is no longer required.