- #1
ChrisVer
Gold Member
- 3,378
- 465
I am not sure whether it should be here, or in statistical mathematics or in computers thread...feel free to move it. I am using it here because I am trying to understand the algorithm when it's used in particle physics (e.g. identification of neutral pions in ATLAS).
As I read it:
In general we have a some (correlated) discriminating variables and we want to combine them into one more powerful discriminant. For that we use the Boost Decision Tree (BDT) method.
The method is trained with an input of signal (cluster closest to each [itex]\pi^0[/itex] with some selection of the cluster-pion distance [itex]\Delta R <0.1[/itex]) and background samples (the rest).
The training starts by applying a one-dimensional cut on the variable that provides the best discrimination of the signal and background samples.
This is subsequently repeated in both the failed and succeeded sub-samples using the next more powerful variable, until the number of events in a certain subsample has reached a minimum number of objects.
Objects are then classified as signal or background dependent on whether they are in a signal or background-like subsample. The result defines a tree.
The process is repeated weighting wrongly classified candidates higher (boosting them), and it stops when the number of pre-defined trees has been reached. And the output is the likelihood estimator of whether the object is signal or background.
My questions:
Taking a discrimination for the best discriminating variable, the algorithm will check whether some variable cut is satisfied and will lead to YES or NO.
Then to the resulting two boxes, another check is going to be done with some other variable. And so on... However I don't understand how this can stop somewhere and not keep going until all the variables are checked (I don't understand then the: "until the number of events in a certain subsample has reached a minimum number of objects").
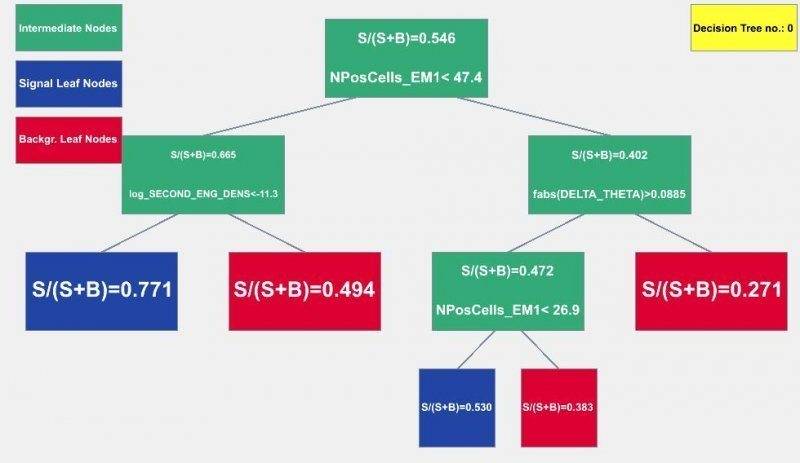
A picture of what I am trying to explain is shown below (the weird names are just the names of the variables, S:signal, B:background):
As I read it:
In general we have a some (correlated) discriminating variables and we want to combine them into one more powerful discriminant. For that we use the Boost Decision Tree (BDT) method.
The method is trained with an input of signal (cluster closest to each [itex]\pi^0[/itex] with some selection of the cluster-pion distance [itex]\Delta R <0.1[/itex]) and background samples (the rest).
The training starts by applying a one-dimensional cut on the variable that provides the best discrimination of the signal and background samples.
This is subsequently repeated in both the failed and succeeded sub-samples using the next more powerful variable, until the number of events in a certain subsample has reached a minimum number of objects.
Objects are then classified as signal or background dependent on whether they are in a signal or background-like subsample. The result defines a tree.
The process is repeated weighting wrongly classified candidates higher (boosting them), and it stops when the number of pre-defined trees has been reached. And the output is the likelihood estimator of whether the object is signal or background.
My questions:
Taking a discrimination for the best discriminating variable, the algorithm will check whether some variable cut is satisfied and will lead to YES or NO.
Then to the resulting two boxes, another check is going to be done with some other variable. And so on... However I don't understand how this can stop somewhere and not keep going until all the variables are checked (I don't understand then the: "until the number of events in a certain subsample has reached a minimum number of objects").
A picture of what I am trying to explain is shown below (the weird names are just the names of the variables, S:signal, B:background):