Boundary condition: null traction on the boundary of an elastic block

[bobinthebox]

Hi everyone,

I'm trying to understand the rationale behind the boundary condition for the problem "Finite bending of an incompressible elastic block". (See here from page 180).


Here we have as Cauchy Stress tensor (see eq. (5.82)):

$T = - \pi I + \mu (\frac{l_0^2}{4 \bar{\theta}^2 r^2} e_r \otimes e_r + \frac{4 \bar{\theta}^2} r^2{l_0^2} e_{\theta} \otimes e_{\theta}- I)$

At page 183, in order to impose null traction on the curved boundaries, the author writes

$T_r(r_i) = T_{r_i + h}=0$

I'm having some troubles on how to interpret geometrically the first one of the two above conditions. I'll add a sketch hereafter.

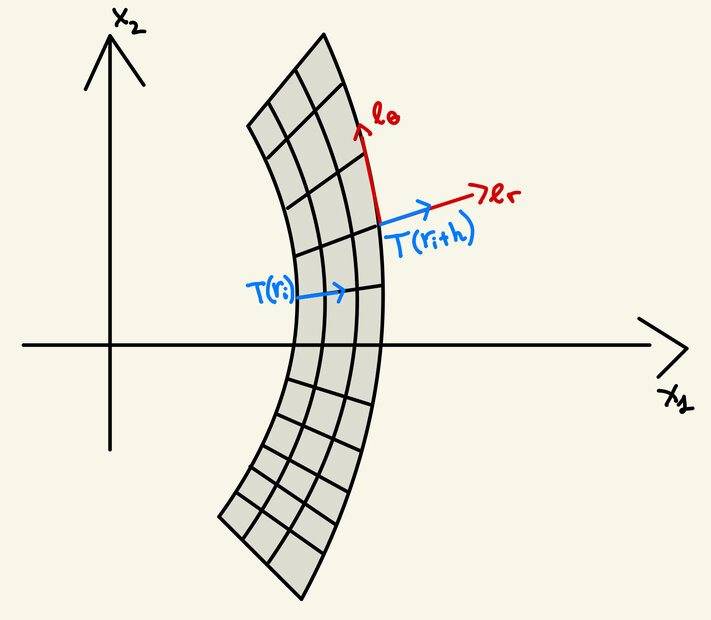My guess is that, since #T_r# is the normal stress (i.e. in #e_r# direction), I'd say that the direction of traction is the same in both conditions, and the only thing that changes is that the evaluation is performed at different radius. In my understanding, what the author wants to impose is that those two blue arrows have 0 length, i.e. the normal component of the stress is identically 0. Is this correct?

Is that right?

 

[Chestermiller]

No. Null traction means that both the normal stress and the shear stress are zero. Also, the inner blue arrow should be flipped.

 

[bobinthebox]

@Chestermiller Thanks for your answer.
So the author doesn't impose explicitely $T_{r \theta} = 0$ because they're already zero, right?


Another thing: I agree with you that the inner blue arrow should be flipped. But $T_r(r_i)= e_r \cdot T(r_i) e_r$ and I don't see how it can be flipped, from this computation.

 

[bobinthebox]

I've tried to solve by myself the second question. I'd be really happy to have your feedback about this. Let's say that I want to impose null normal stress at $r=r_i$.

The normal versor there is $-e_r$, so I should impose $-e_r \cdot T(r_i)(-e_r)=0$ because I want to know the projection in direction $-e_r$ of the stress with outward normal $-e_r$. Now, by the Cauchy thm. we have $T(-n)=-T(n)$ and hence the condition reads $-e_r \cdot -(T(r_i)e_r)=0$ which is equivalent to $T_r(r_i)=0$ which is indeed what the author asks. Is my argument correct?

 

[bobinthebox]

@Chestermiller Did I wrote my last argument too badly to be answered? Let me know if I was not clear enough

 

[Chestermiller]

@Chestermiller Thanks for your answer.
So the author doesn't impose explicitely $T_{r \theta} = 0$ because they're already zero, right?


Another thing: I agree with you that the inner blue arrow should be flipped. But $T_r(r_i)= e_r \cdot T(r_i) e_r$ and I don't see how it can be flipped, from this computation.

You need to dot it with $-e_r$ to get the traction on the surface. This follows from the Cauchy stress relationship.

 

[Chestermiller]

I've tried to solve by myself the second question. I'd be really happy to have your feedback about this. Let's say that I want to impose null normal stress at $r=r_i$.

The normal versor there is $-e_r$, so I should impose $-e_r \cdot T(r_i)(-e_r)=0$ because I want to know the projection in direction $-e_r$ of the stress with outward normal $-e_r$. Now, by the Cauchy thm. we have $T(-n)=-T(n)$ and hence the condition reads $-e_r \cdot -(T(r_i)e_r)=0$ which is equivalent to $T_r(r_i)=0$ which is indeed what the author asks. Is my argument correct?

Yes. Much better.

 

[Chestermiller]

The traction vector at ri is $$-T_{rr}e_r-T_{r\theta}e_\theta$$

NEVER MIND. I see from your representation of the stress tensor that the principal axes of stress are aligned with the coordinate directions, so the shear stress components are zero.

 

[bobinthebox]

Yes, because you used the fact that $T(-n) = -T(n)$, where now $n = e_r$. Since $T e_r = T_{rr} e_r + T_{r \theta} e_{\theta}$ and the normal at $r= r_i$ is $-e_r$ we have

$T(-e_r)=-T(e_r)=-T_{rr} e_r - T_{r \theta} e_{\theta}$, as you wrote. I feel like I got it now.


@Chestermiller I have a really last question about the imposition of boundary conditions.

Assume we're using first Piola-Kirchoff stress tensor in order to solve the problem. It is defined at (5.83) in the link I posted above. In order to impose null traction on the curved boundaries the author writes

$S_{r1}(\pm \frac{h_0}{2})=0$

(equation (5.100))

But I can't see the meaning of $S_{r1}$. I only understand that the evaluation at $\pm \frac{h_0}{2}$ is needed to act on the curved boundaries, but have no idea about why I have to use component $S_{r1}$.