Redwaves
- 134
- 7
- Homework Statement
- The boundary conditions for 2 ropes fixed to a massless ring with a massless damper
A wave comes from the left (rope 1) to the right (rope 2).
- Relevant Equations
- ##\psi_1 = Ae^{i(\omega t -k_1x)} + Re^{i(\omega t + k_1x)}##
##\psi_2 = Te^{i(\omega t -k_2x)}##
Hi,
I'm not quite sure if I'm correct. I need to find the boundary conditions for 2 ropes ##T_1 \mu_1, T_2 \mu_2## fixed at ##x=0## to a massless ring with a massless damper of force ##F_d - -bv_y##
Here what I think, since the ring and the damper is massless ##\sum F_y = 0##. Thus, ##-T_1 \frac{\partial \psi_1}{\partial x} + T_2 \frac{\partial \psi_2}{\partial x} -b \frac{dy}{dt} = 0##
Then, the height must be the same for the first rope, the ring and the second rope at ##x=0##, thus ##y_d = \psi_1(0,t) = \psi_2(0,t)##
Which mean, A + R = T, since ##Ae^{i(\omega t -k_1x)} + Re^{i(\omega t + k_1x)} = Te^{i(\omega t -k_2x)}## at x=0
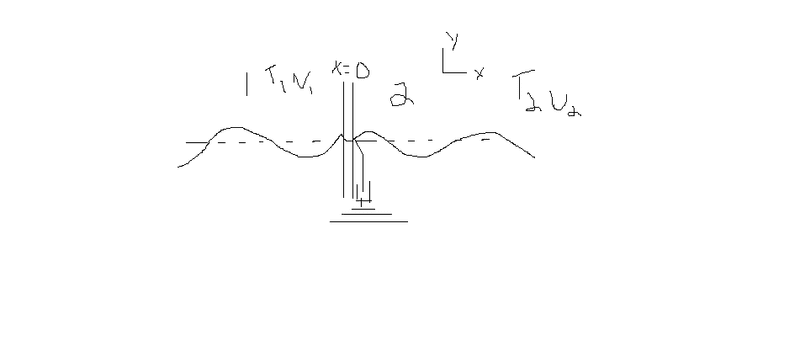
I'm not quite sure if I'm correct. I need to find the boundary conditions for 2 ropes ##T_1 \mu_1, T_2 \mu_2## fixed at ##x=0## to a massless ring with a massless damper of force ##F_d - -bv_y##
Here what I think, since the ring and the damper is massless ##\sum F_y = 0##. Thus, ##-T_1 \frac{\partial \psi_1}{\partial x} + T_2 \frac{\partial \psi_2}{\partial x} -b \frac{dy}{dt} = 0##
Then, the height must be the same for the first rope, the ring and the second rope at ##x=0##, thus ##y_d = \psi_1(0,t) = \psi_2(0,t)##
Which mean, A + R = T, since ##Ae^{i(\omega t -k_1x)} + Re^{i(\omega t + k_1x)} = Te^{i(\omega t -k_2x)}## at x=0
Last edited: