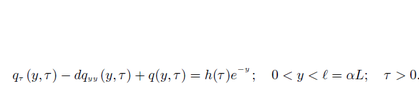Boundary conditions of dirichlet problem

[simo1]

the boundary conditions on p are homogenous dirichlet on this equation
View attachment 2369

where q(0,τ)=0 and q(l,t)=0 for all τ>0.
the initial condition p(x,0)=p_o(x) also translates to an initial condition on p. how do i show what the new initial condition is on q

 

[jvicens]

To show the new initial condition on q, we can use the fact that the initial condition on p translates to an initial condition on q. This means that at time t=0, we have q(x,0) = -p_t(x,0) = -p_o'(x). Since q(0,τ)=0, this also means that q(x,0) = 0 for all x in the domain. Therefore, the new initial condition on q is q(x,0) = 0 for all x in the domain. This can also be written as q(x,0) = q_o(x), where q_o(x) is the initial condition on q.