Boundary finite element method in Maple

[Charles95]

TL;DR Summary

Fix Maple error in a home made program on Maple

I would like any tips about a Maple ''home made'' program that I received for a project but this program seems to stop before the very end of the code. I want to find de lift of an airfoil with Boundary finites elements method. I have this error at the very end :
Error, (in fprintf) number expected for floating point format. This code is very long, so I don't want to send all of it. I sent the code lines at the end of the program and the text is in french if you need to translate. The program want to find the speed potential, his derivative, the pressure at the extrados and intrados and finally the lift and lift coefficient. I also think that this error occurs near the end of the code for the printing of results. So here is five pictures that resume the end of the program which think would be related to my error. Is someone can help me?

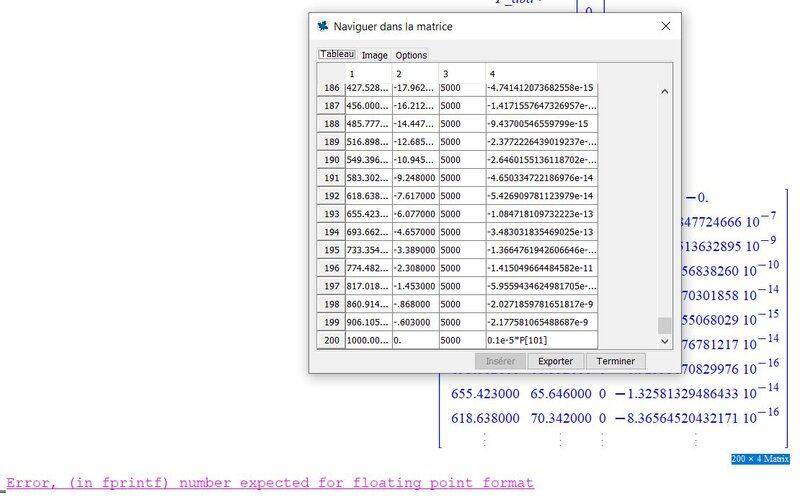
As you can see for the point #200 it doesn't calculate the last Pressure value and I think it's the reason why the programm doesn't calculate the lift of the airfoil as supposed in picture #3.
Vp is speed perturbated, Vinf is speed at infinity in the domain far from the airfoil. X, Y ,Z are coordinates on the airfoil boundary. If you need any informations please ask me.

Thank you very much!

 

[DrClaude]

The problem appears to come from the line

P_aba[i]:=1E-6*P[k]

when k=101. I suspect that P has a dimension of 100 (is N=100?).

 

[Charles95]

Yes N = 100. What do I need to change? I'm not very good in programming, but if I change P[k] to P[k-1] or P_aba to P_aba[i-1] could it solves my problem?

Thanks!

 

[DrClaude]

Yes N = 100. What do I need to change? I'm not very good in programming, but if I change P[k] to P[k-1] or P_aba to P_aba[i-1] could it solves my problem?

Thanks!

If by solving the problem, you mean "get rid of the error message," then yes. If instead you mean "get the correct answer," then probably not.

Fixing this will require going back to the original equations and figuring out what is going wrong.

 

[Charles95]

If by solving the problem, you mean "get rid of the error message," then yes. If instead you mean "get the correct answer," then probably not.

Fixing this will require going back to the original equations and figuring out what is going wrong.

I would like to fix both, but when I write P[k-1] it put the error at the beginning of the vector result. So it means that at P[0] I get the error 0.1E-05*P[0] instead of 0.1E-05*P[101]. How should I fix that? I would like to solve the problem for the correct answer, but I just don't know how we could proceed so I guess I need to turn back to my teacher...