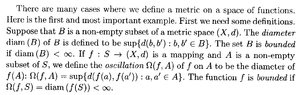Bounded in Norm .... Garling, Section 11.2: Normed Spaces ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help with some remarks by Garling concerning a subset being norm bounded of bounded in norm ...

The particular remarks by Garling read as follows:View attachment 8950
Note that the definition of a bounded set by Garling is included in the following text:
View attachment 8951
In the remarks by Garling above we read the following:

" ... ... Then since

$$\mid \mid x - y \mid \mid \le \mid \mid x \mid \mid + \mid \mid y \mid \mid$$ and $$\mid \mid y \mid \mid \le \mid \mid y - x \mid \mid + \mid \mid x \mid \mid$$

a subset $$B$$ is bounded if and only if $$\text{sup } \{ \mid \mid b \mid \mid \ : \ b \in B \} \lt \infty$$ ... ... ... "Can someone please explain/demonstrate how (given Garling;s definition of a bounded subset) that the statements:

$$\mid \mid x - y \mid \mid \le \mid \mid x \mid \mid + \mid \mid y \mid \mid$$ and $$\mid \mid y \mid \mid \le \mid \mid y - x \mid \mid + \mid \mid x \mid \mid$$

lead to the statement that:

a subset $$B$$ is bounded if and only if $$\text{sup } \{ \mid \mid b \mid \mid \ : \ b \in B \} \lt \infty$$ ... ... ... ?Hope someone can help ...

Peter

======================================================================================

It may help some readers of the above post to have access to the start of Garling's section on normed spaces in order to familiarize them with Garling's approach and notation ... so I am providing the same ... as follows:View attachment 8952Hope that helps ...

Peter

 

[Olinguito]

$E$ is both a metric space and a vector space; the metric and the norm are related by
$$d(x,y)\ =\ \|x-y\|$$
for $x,y\in E$.

So if $B\subset E$ is nonempty – say it contains $c$ – and bounded, we have for all $b\in B$,
$$\|b\|\ \le\ \|b-c\|+\|c\|\ \le\ \text{diam}(B)+\|c\|$$
$\displaystyle\implies\ \sup_{b\in B}\|b\|<\infty$ (since $\text{diam}(B)<\infty$ and $\|c\|$ is a fixed number). Conversely, if $\displaystyle s=\sup_{b\in B}\|b\|<\infty$, then for all $b,b'\in B$,
$$d(b,b')\ =\ \|b-b'\|\ \le\ \|b\|+\|b'\|\ \le\ 2s$$
$\implies\ \text{diam}(B)<\infty$.

 

[Math Amateur]

$E$ is both a metric space and a vector space; the metric and the norm are related by
$$d(x,y)\ =\ \|x-y\|$$
for $x,y\in E$.

So if $B\subset E$ is nonempty – say it contains $c$ – and bounded, we have for all $b\in B$,
$$\|b\|\ \le\ \|b-c\|+\|c\|\ \le\ \text{diam}(B)+\|b'\|$$
$\displaystyle\implies\ \sup_{b\in B}\|b\|<\infty$ (since $\text{diam}(B)<\infty$ and $\|c\|$ is a fixed number). Conversely, if $\displaystyle s=\sup_{b\in B}\|b\|<\infty$, then for all $b,b'\in B$,
$$d(b,b')\ =\ \|b-b'\|\ \le\ \|b\|+\|b'\|\ \le\ 2s$$
$\implies\ \text{diam}(B)<\infty$.

Thanks for the help Olinguito ...

But ... just a clarification ...

You write: $$\|b\|\ \le\ \|b-c\|+\|c\|\ \le\ \text{diam}(B)+\|b'\|$$

Did you mean $$\|b\|\ \le\ \|b-c\|+\|c\|\ \le\ \text{diam}(B)+\|c\|$$ ... ... ?
Thanks again ...

Peter

 

[Olinguito]

Yes, I did. I’ve fixed the post now.

 

[Math Amateur]

Yes, I did. I’ve fixed the post now.

Thanks again for your help ...

Peter

 

[Math Amateur]

$E$ is both a metric space and a vector space; the metric and the norm are related by
$$d(x,y)\ =\ \|x-y\|$$
for $x,y\in E$.

So if $B\subset E$ is nonempty – say it contains $c$ – and bounded, we have for all $b\in B$,
$$\|b\|\ \le\ \|b-c\|+\|c\|\ \le\ \text{diam}(B)+\|c\|$$
$\displaystyle\implies\ \sup_{b\in B}\|b\|<\infty$ (since $\text{diam}(B)<\infty$ and $\|c\|$ is a fixed number). Conversely, if $\displaystyle s=\sup_{b\in B}\|b\|<\infty$, then for all $b,b'\in B$,
$$d(b,b')\ =\ \|b-b'\|\ \le\ \|b\|+\|b'\|\ \le\ 2s$$
$\implies\ \text{diam}(B)<\infty$.

Just returned to this thread with another question ...

It has been shown above that $$\text{diam} (B) \lt \infty$$ follows from $$\mid \mid y \mid \mid \le \mid \mid y - x \mid \mid + \mid \mid x \mid \mid$$ alone ...

... so why does Garling mention $$\mid \mid x - y \mid \mid \le \mid \mid x \mid \mid + \mid \mid y \mid \mid$$ Help will be appreciated ...

Peter*** EDIT ***

Oh! The other inequality is needed for the converse ... sorry ... should have read your post more carefully ...

Peter