- #1
Chem.Stud.
- 27
- 2
Bragg's Law is well-known, and looks like the following:
[itex] nλ = 2d \cdot sin(θ) [/itex], where d is the distance between the two crystal planes.
This equation, or criteria, describes when constructive interference happens and an intensified, reflected ray can be measured at the same angle as the incoming rays. The equation is motivated based on Figure 1 below.
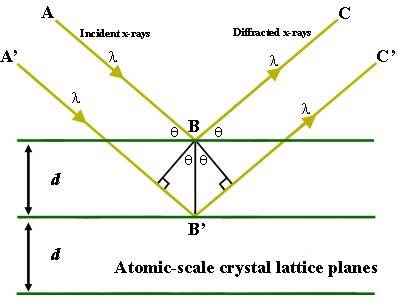
Figure 1. Two x-rays hitting and reflecting off of two different high-electron-density planes in a crystal. Outgoing rays are parallel.
Something has puzzled me about this figure. The rays are parallel and not overlapping. The ray going deeper into the crystal travels farther than the other ray, and this distance has to be a whole integer's multiplum of the wave length to ensure constructive interference. But the outgoing rays are parallel and have no reason to interact; they should be overlapping. So let us consider (the poor freehand) Figure 2, in which the outcoming rays actually overlap and are able to interact (special case of [itex]45 ^{\circ} [/itex] incoming rays).
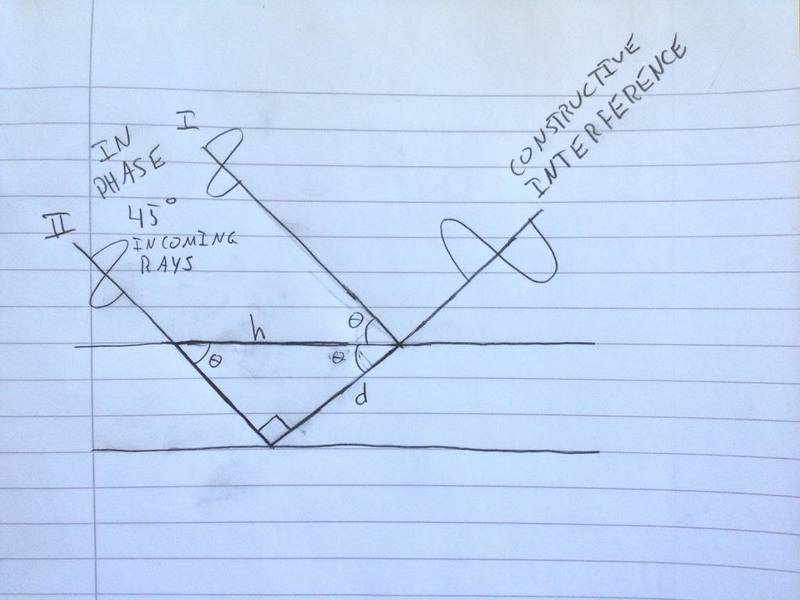
Figure 2. Outgoing rays overlap, which is necessary for constructive interference. d represents the distance ray II has to travel farther than ray 1. h is the hypotenuse, and also the distance between the points where the two rays penetrate or reflect off the first plane.
Following Figure 2, the equation becomes [itex]nλ = h \cdot sin(θ) [/itex]. At other angles than 45 degrees, the equation becomes [itex] nλ = 2d \cdot sin(θ)cos(θ) [/itex], where d is the distance ray II has to travel farther than ray 1 has to travel.
Can the model in Figure 1 be extended to overlapping outgoing rays? Surely, since the entire x-ray diffraction method is based on Figure 1, something must be correct. But why is the principles always explained by showing two parallel outgoing rays, when they should indeed overlap? Because that is the whole point, is it not; the bragg criteria must be fulfilled in order for outgoing rays to be reflected off in phase?
I hope I have explained my thoughts sufficiently for someone to help me out.
Anders
[itex] nλ = 2d \cdot sin(θ) [/itex], where d is the distance between the two crystal planes.
This equation, or criteria, describes when constructive interference happens and an intensified, reflected ray can be measured at the same angle as the incoming rays. The equation is motivated based on Figure 1 below.
Figure 1. Two x-rays hitting and reflecting off of two different high-electron-density planes in a crystal. Outgoing rays are parallel.
Something has puzzled me about this figure. The rays are parallel and not overlapping. The ray going deeper into the crystal travels farther than the other ray, and this distance has to be a whole integer's multiplum of the wave length to ensure constructive interference. But the outgoing rays are parallel and have no reason to interact; they should be overlapping. So let us consider (the poor freehand) Figure 2, in which the outcoming rays actually overlap and are able to interact (special case of [itex]45 ^{\circ} [/itex] incoming rays).
Figure 2. Outgoing rays overlap, which is necessary for constructive interference. d represents the distance ray II has to travel farther than ray 1. h is the hypotenuse, and also the distance between the points where the two rays penetrate or reflect off the first plane.
Following Figure 2, the equation becomes [itex]nλ = h \cdot sin(θ) [/itex]. At other angles than 45 degrees, the equation becomes [itex] nλ = 2d \cdot sin(θ)cos(θ) [/itex], where d is the distance ray II has to travel farther than ray 1 has to travel.
Can the model in Figure 1 be extended to overlapping outgoing rays? Surely, since the entire x-ray diffraction method is based on Figure 1, something must be correct. But why is the principles always explained by showing two parallel outgoing rays, when they should indeed overlap? Because that is the whole point, is it not; the bragg criteria must be fulfilled in order for outgoing rays to be reflected off in phase?
I hope I have explained my thoughts sufficiently for someone to help me out.
Anders