- #1
Apashanka
- 429
- 15
The brans-dicke action is
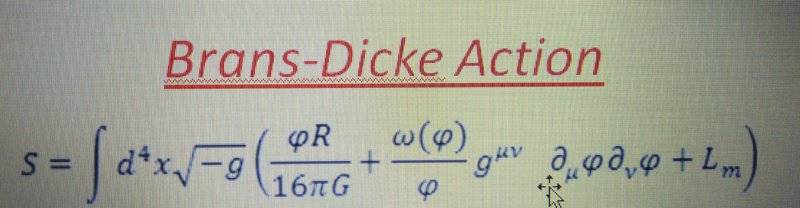
We have R which contains second order derivative in space and time of the metric components and product of first order derivatives in space and time of the metric components .
The second term in the figure also contains product of first order derivatives in space and time of the scaler field Φ(x,t).
To make it dimensionally consistent if we consider that the metric components gij vary over space, but how can be it is a function of time??
It is only if the space is curved for which locally the metric components gij doesn't vary locally but on a large scale (globally)on the manifold it varies (e.g gij(x) and if the space is expanding e.g gij(t) .
Is it so??
We have R which contains second order derivative in space and time of the metric components and product of first order derivatives in space and time of the metric components .
The second term in the figure also contains product of first order derivatives in space and time of the scaler field Φ(x,t).
To make it dimensionally consistent if we consider that the metric components gij vary over space, but how can be it is a function of time??
It is only if the space is curved for which locally the metric components gij doesn't vary locally but on a large scale (globally)on the manifold it varies (e.g gij(x) and if the space is expanding e.g gij(t) .
Is it so??
Attachments
Last edited: