- #1
thissong
- 5
- 2
I am trying to design a drive shaft that breaks when i apply a specific torque to protect fro over torquing. I made a few samples, and now i am trying to compare the results to my equations. My problem is, none of the equations seem to match the actual results. Your help would be appreciated:
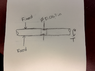
I made a bar that was 0.078in. in diameter, necked it down to 0.067in. diameter (.0335in. radius)
In testing, I found that the bar shears/breaks at around 9.6 in-lbs.
τ = T*r/J = 9.6in-lbs*.0335in/((π/2)*.0335in^4) = 164ksi
Now, my material states that I have an tensile strength of 170 ksi and yield strength of 140 ksi, and i thought, "Great! 3.5% error on my yield strength", but then i remembered the 0.577*σ rule. (making shear stress only .577*170 = 98ksi). I'd expect this to break at 5.7in-lbs using that conversion. Can any explain why my test results don't match up to my theoretical values?
(I considered using a stress concentration factor, but that would only make my answer more puzzling because it would increase the discrepancy where τ(max) = τ(nom)*K and K>1)Thank you
I made a bar that was 0.078in. in diameter, necked it down to 0.067in. diameter (.0335in. radius)
In testing, I found that the bar shears/breaks at around 9.6 in-lbs.
τ = T*r/J = 9.6in-lbs*.0335in/((π/2)*.0335in^4) = 164ksi
Now, my material states that I have an tensile strength of 170 ksi and yield strength of 140 ksi, and i thought, "Great! 3.5% error on my yield strength", but then i remembered the 0.577*σ rule. (making shear stress only .577*170 = 98ksi). I'd expect this to break at 5.7in-lbs using that conversion. Can any explain why my test results don't match up to my theoretical values?
(I considered using a stress concentration factor, but that would only make my answer more puzzling because it would increase the discrepancy where τ(max) = τ(nom)*K and K>1)Thank you