- #1
- 2,355
- 10
[size=+]I. Introduction[/size]
With great sadness I note the passing of one of the Best Things Ever: a few days ago, John Baez posted the final installment (Week 300) in his long-running internet column, This Week's Finds in Mathematical Physics.
But John himself is not sad; he is desperate--- to save the world. See Week 300 for his own explanation, and note that his various blogs and writings will continue, but focusing on extra-mathematical topics.
What does this have to do with the Rubik cube? Well, the topic of Week 300 happens to be very closely related to one of my own interests, the theory of "combinatorial species", a subject created by Andre Joyal using the notions of category theory. One way to try to briefly encapsulate what this theory is all about is to say that an old and often reinvented idea in mathematics involves working with "points" which have been endowed with some kind of "structure", and then two fundamental problems are:
The theory of "combinatorial species" forms part of the background needed to appreciate another major but under-reported recent event: a group of researchers claimed to have established (via computer) that in the Rubik group (the symmetry group of the 3x3x3 Rubik cube), every element can be expressed in terms of the six standard generators and their inverses using at most 20 words in the "face turn metric", which counts [itex]f, f^2, f^3 = f^{-1}[/itex] as one face turn, where [itex]f[/itex] is a clockwise quarter-turn of the front face (in a standard notation due to Singmaster). I wrote "claimed to have established" because the work has not yet been published, but the authors are leaders in this field and have previously published papers on the same topic, so there is a very good chance their claim is correct.
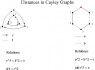
As I write, the Wikipedia articles which mention this development are not quite right, since they confuse the "face turn metric" with the "quarter turn metric" in which [itex]f^{\pm1}[/itex] counts as one move but [itex]f^2[/itex] counts as two moves. The face turn metric is closer to the experience of "cubers" manipulating a physical Rubik's cube, but the quarter-turn metric is the one which is directly related to the question: what is the diameter of the Cayley graph of the Rubik group with the six standard generators by quarter turns of the six faces [itex]u, \, f, \, r, \, l, \, b, \,d[/itex] (up, front, right, left, back, down). This problem has been unsolved for 30 years, since it was first asked by David Singmaster! Results about the maximal number of moves in either the face-turn or quarter-turn metric required to express elements of the Rubik group can be considered alternative ways of answering the question: how much better is "God's algorithm" for solving the Rubik cube than the algorithms used by the best human "speedcubers"?
The problems of determining the maximal shortest word in the face turn and quarter turn metrics are certainly distinct, since it has been known for some time that the "superflip" (a particular interesting element of the Rubik group) requires 20 moves in the face-turn metric (so that, according to the new result, this element belongs to the set of rather rare elements which require the maximal number of moves in the face-turn metric), but another element, "superflip with four-spot" requires more moves in the quarter-turn metric than does the superflip. AFAIK, the best current result--- it's due to Tomas Rokicki, a coauthor of the research in question--- for the quarter-turn metric is that every element of the Rubik group can be expressed using at most 29 turns in the q-turn metric. However, AFAIK, Rokicki conjectures that the diameter of the Cayley graph of the Rubik group with the six quarter-turn generators is in fact 26.
In this thread, I hope to provide some background needed to appreciate statements about the Rubik group. At the very least, I hope to provide
An ironical detail: I don't possesses a physical Rubik cube, and due to concerns about Java script, I can't access the many on-line tutorials which use Java script to describe alleged "solutions of the cube". So my knowledge of "cubing" is (so far) entirely theoretical!
my knowledge of "cubing" is (so far) entirely theoretical!
With great sadness I note the passing of one of the Best Things Ever: a few days ago, John Baez posted the final installment (Week 300) in his long-running internet column, This Week's Finds in Mathematical Physics.
But John himself is not sad; he is desperate--- to save the world. See Week 300 for his own explanation, and note that his various blogs and writings will continue, but focusing on extra-mathematical topics.
What does this have to do with the Rubik cube? Well, the topic of Week 300 happens to be very closely related to one of my own interests, the theory of "combinatorial species", a subject created by Andre Joyal using the notions of category theory. One way to try to briefly encapsulate what this theory is all about is to say that an old and often reinvented idea in mathematics involves working with "points" which have been endowed with some kind of "structure", and then two fundamental problems are:
- how do you count "structured points"?
- how do you permute "structured points"?
The theory of "combinatorial species" forms part of the background needed to appreciate another major but under-reported recent event: a group of researchers claimed to have established (via computer) that in the Rubik group (the symmetry group of the 3x3x3 Rubik cube), every element can be expressed in terms of the six standard generators and their inverses using at most 20 words in the "face turn metric", which counts [itex]f, f^2, f^3 = f^{-1}[/itex] as one face turn, where [itex]f[/itex] is a clockwise quarter-turn of the front face (in a standard notation due to Singmaster). I wrote "claimed to have established" because the work has not yet been published, but the authors are leaders in this field and have previously published papers on the same topic, so there is a very good chance their claim is correct.
As I write, the Wikipedia articles which mention this development are not quite right, since they confuse the "face turn metric" with the "quarter turn metric" in which [itex]f^{\pm1}[/itex] counts as one move but [itex]f^2[/itex] counts as two moves. The face turn metric is closer to the experience of "cubers" manipulating a physical Rubik's cube, but the quarter-turn metric is the one which is directly related to the question: what is the diameter of the Cayley graph of the Rubik group with the six standard generators by quarter turns of the six faces [itex]u, \, f, \, r, \, l, \, b, \,d[/itex] (up, front, right, left, back, down). This problem has been unsolved for 30 years, since it was first asked by David Singmaster! Results about the maximal number of moves in either the face-turn or quarter-turn metric required to express elements of the Rubik group can be considered alternative ways of answering the question: how much better is "God's algorithm" for solving the Rubik cube than the algorithms used by the best human "speedcubers"?
The problems of determining the maximal shortest word in the face turn and quarter turn metrics are certainly distinct, since it has been known for some time that the "superflip" (a particular interesting element of the Rubik group) requires 20 moves in the face-turn metric (so that, according to the new result, this element belongs to the set of rather rare elements which require the maximal number of moves in the face-turn metric), but another element, "superflip with four-spot" requires more moves in the quarter-turn metric than does the superflip. AFAIK, the best current result--- it's due to Tomas Rokicki, a coauthor of the research in question--- for the quarter-turn metric is that every element of the Rubik group can be expressed using at most 29 turns in the q-turn metric. However, AFAIK, Rokicki conjectures that the diameter of the Cayley graph of the Rubik group with the six quarter-turn generators is in fact 26.
In this thread, I hope to provide some background needed to appreciate statements about the Rubik group. At the very least, I hope to provide
- a tutorial on using GAP to define and play around with the Rubik group and some related groups, including at least a sketch of how you can start working out your very own algorithm for solving the Rubik cube puzzle,
- essential (?) background:
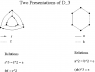
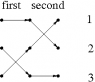
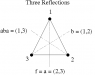
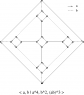
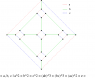
- a brief illustrated explanation of Cayley graphs and a related concept, Schreier graphs,
- the principle result concerning the Rubik group, the structure theorem of Ann Scott which expresses it as a specific index 12 subgroup of the group
[tex]
\left( C_3 \wr S_8 \right) \times \left( C_2 \wr S_{12} \right)
[/tex]
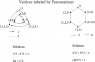
which is the direct product of two generalized permutation groups (if you haven't seen this before, but guess it has something to do with "independent" generalized permutations of the eight "corner cubies" and the twelve "edge cubies", you guess correctly!), - a tutorial on wreath products--- a construction giving an answer (actually, two answers) to the question: "how do you permute structured points?"--- particularly the case of generalized symmetric groups and generalized alternating groups, including
- a "fiber-bundle" picture related to Kleinian geometry,
- the Frobenius cocycle and how we can use that to construct a Cayley graph from the Schreier graphs associated with a (possibly not subnormal) series of nested subgroups of G,
- the "restoration problem" for generalized symmetric/alternating groups
- some background on the major problems of computational group theory and how most of them can be efficiently solved,
- some background on group theory generally, particularly
- the intuitive meaning of conjugate elements, conjugate subgroups, cosets, and commutator elements in a given group,
- actions by a given group G and the category of G-sets, including the basic structure theorems,
- permutation representations of groups vs. linear representations of groups,
- some background on the theory of "random permutations" drawn from a given permutation group, in particular symmetric/alternating groups and the Rubik group, plus a tutorial on using GAP to gather (reliable) statistics about possibly huge finite permutation groups,
- some background on combinatorial group theory, including generators and relations, and the problem of "translating" words expressed with respect using one generating set to an equivalent word expressed using another generating set, mentioning some fundamental and open problems for the Rubik group,
- some background on Kleinian geometry, needed to fully appreciate the "fiber-bundle" picture associated with wreath products, possibly also discussion of some small examples of finite projective spaces, affine spaces, finite analogs of euclidean geometry, etc.,
- some background on Wille's "concept theory", which applies to any relation (so very general), is easy to use and learn, and often provides useful insight, so IMO it deserves to be better known,
- since a sequence of finite constructions is often best understood in terms of a single countable construction, some background on oligomorphic permutation groups, homogeneous countable graphs and the Erdos-Renyi "universal (countable) random graph",
- some background on an information theory "unifying" Boltzmann's notion of entropy (microstates and macrostates) with Galois theory, which (given an action by a group G on a set X) answers the question: "what information is required to say how the points of a subset A of X are moved by an element g, if we know how the points of another possibly disjoint subset B are moved by g?".
- Wikipedia and its ills,
- the workings of the New Panopticon, including the public-private partnership between multinational spycos (a category in which I include Google) and secret police agencies of various states.
An ironical detail: I don't possesses a physical Rubik cube, and due to concerns about Java script, I can't access the many on-line tutorials which use Java script to describe alleged "solutions of the cube". So
Last edited: