Building a logic circuit from a truth table

[MarcL]

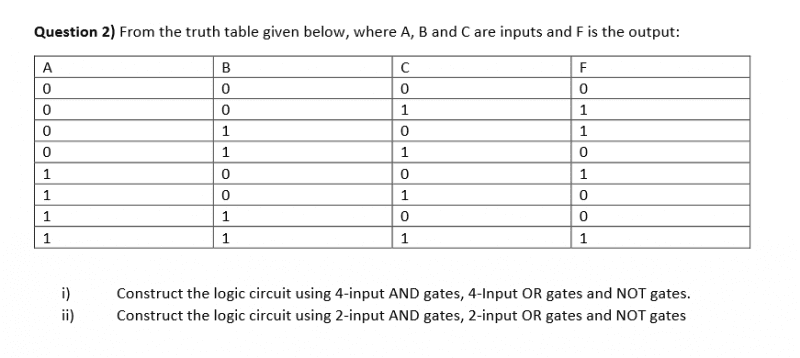
P.S I know I am not supposed to use attachment but there are no way for me to input the table in a clean way... same for the logic circuit drawing. Would anyone mind helping me?

1. Homework Statement

Homework Equations

AND gates require both input to be True to get a true ouput
NOT gates are just the opposite of what you input in them ( 1 -- > 0 and 0 --> 1)
OR gates require at least one input to be true to create a true output

The Attempt at a Solution

I can't seem to understand why the answer key uses 4 AND gates with 3 output. Like the one below :

It just seems very... weird that there are only 4 a inputs where as in the truth table there are 8 inputs in the truth table. Anybody can help me understand that?

 

[berkeman]

Have you drawn a Karnaugh Map for that truth table? Can you share it with us? :-)

 

[MarcL]

Oh, well I know how, I just didn't try because this was a set of problems before it was taught, but I'll do that right now. ^^

 

[Mark44]

It just seems very... weird that there are only 4 a inputs where as in the truth table there are 8 inputs in the truth table.

There are four inputs in the truth table -- A, B, C, and F -- not eight.

Edit: Make that three inputs -- A, B, and C --and one output -- F.

 

[MarcL]

So I'm guessing the first thing to do is reduce the truth table either using theorems or karnaugh map right? ( hence why you asked)... If so then I got the following

FAB 00 01 11 10
C
0 0 1 0 1
1 1 0 1 0
and then I group together if I remember correctly and that allows me to cancel the input that "changes" if the input is the same ( I don't know if I'm clear? :/). But none of them are similar.

Edit: Sorry I didn't express myself right... I meant 8 possibilities out of 3 inputs ( 2^3)
Edit2: Can't seem to format this table right ughhhh

 

[berkeman]

Edit2: Can't seem to format this table right ughhhh

Try using the "code" tags to preserve spaces for formatting. Like this:

A B C D
0 1 0 1

 

[MarcL]

  AB      00  01  11  10
C
0          0   1   0   1
1          1   0   1   0

Thanks!

 

[berkeman]

Wow, doesn't look like there are any simplifications. That's why there are 4 separate minterms that you OR together to get the output.

 

[NascentOxygen]

@MarcL Has your question now been answered?

As an aside, if you were allowed to use any gates of your choosing, you'd just need a pair of 2-input exclusive-ORs.

F = A ⊕ (B⊕C)

 

[berkeman]

F = A ⊕ (B⊕C)

Nice! Too bad he can't use XORs. I'll remember that trick! :-)

 

[LCKurtz]

Edit2: Can't seem to format this table right ughhhh

You can do nice K map tables in Latex:$$
\begin{array}{|c|c|c|c|c|}
\hline C|AB & 00 & 01 & 11 & 10\\
\hline 0&0&1&0&1\\
\hline 1 & 1 & 0 & 1 & 0\\
\hline
\end{array}$$