Buoyant Force and Archimedes' Principle

[EnricoHendro]

Homework Statement

The weight of a rectangular block of low-density material is 15.0 N. With a thin string, the center of the horizontal bottom face of the block is tied to the bottom of a beaker partly filled with water. When 25.0% of the block’s volume is submerged, the tension in the string is 10.0 N. (a) Find the buoyant force on the block. (b) Oil of density 800 kg/m3 is now steadily added to the beaker, forming a layer above the water and surrounding the block. The oil exerts forces on each of the four sidewalls of the block that the oil touches. What are the directions of these forces? (c) What happens to the string tension as the oil is added? Explain how the oil has this effect on the string tension. (d) The string breaks when its tension reaches 60.0 N. At this moment, 25.0% of the block’s volume is still below the water line. What additional fraction of the block’s volume is below the top surface of the oil?

Relevant Equations

B=T+Mg
B-Mg-T=0

Hello there, I have a quite different approach on answering the part c and d of this problem. Can you guys help me to see if my method is acceptable or logical? (I got the same answers as the back of the textbook, however my methods differ from the solutions manual). Here is my answer/attempt at a solution :
Part A :
B = T+Mg
B = 25 N
Part B :
Perpendicular to each sides of the block (towards the centre of the block)
Part C :
if the density of the object is less than the density of the fluid, then the object would accelerate upward until it floats which at that point, the object reaches static equilibrium (assuming the liquid does not generate any waves). We see that the density of the object is less than the density of oil. The proof is as follows :

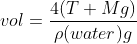
thus, vol = 0.010204081 Meter Cubic. Since :

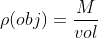, and M = 1.530612245 Kg, therefore, the density of the object is 150 Kg/Meter Cubic.
Therefore, the additional presence of oil would exert a buoyant force towards the remaining part of the cube that is not submerged in water. This increases the tension.

Part D :
B-Mg-T=0

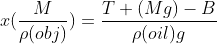
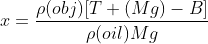
with x being the part of the volume that is under the top surface of oil. Therefore :

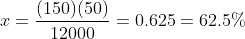
Thus, 25% of the cube is submerged in water, while 62.5% of the volume of the cube is submerged in oil, and the remaining 12.5% of the cube is not submerged in anything.

 

[haruspex]

towards the centre of the block

That could be misinterpreted as meaning directly towards the centre of the block from each point on the surface. Better just to say "inward".

the object would accelerate upward

It's still tethered.

Therefore, the additional presence of oil would exert a buoyant force towards the remaining part of the cube that is not submerged in water.

This is a bit of a trap.
You had just stated that all the forces the oil exerts on the block are horizontal, so how is it exerting a buoyant force?
Archimedes' principle assumes the fluid is able to reach all parts of the surface of the object below the top surface of the fluid.
Can you think of a more persuasive explanation?

 

[EnricoHendro]

That could be misinterpreted as meaning directly towards the centre of the block from each point on the surface. Better just to say "inward".

It's still tethered.

This is a bit of a trap.
You had just stated that all the forces the oil exerts on the block are horizontal, so how is it exerting a buoyant force?
Archimedes' principle assumes the fluid is able to reach all parts of the surface of the object below the top surface of the fluid.
Can you think of a more persuasive explanation?

I see. Thank you for pointing out my mistakes. What about the part D? is my approach of calculating the additional fraction of the volume that is below the top of the surface of oil acceptable? or is it also a wrong approach that happens to have a correct conclusion?

 

[Lnewqban]

I believe that your logic is correct regarding response to d).

This cube is submerged in two different fluids; therefore, it is displacing two volumes of different densities.
The addition of those two weights must be equal to the 75 N of buoyant force.

Consider the profile of pressure distribution for water only, for response to b).
Then, consider the different profiles of pressure distribution for both fluids as submerged depth increases.

Please, see:
https://courses.lumenlearning.com/boundless-physics/chapter/archimedes-principle/

 

[haruspex]

I see. Thank you for pointing out my mistakes. What about the part D? is my approach of calculating the additional fraction of the volume that is below the top of the surface of oil acceptable? or is it also a wrong approach that happens to have a correct conclusion?

Part D is correct, except that you seem to have changed the meaning of B after the first line.

You have not really finished part C. As you say, the tension increases, but you are asked to explain why.
Given that the forces the oil exerts directly on the block are horizontal, why has the buoyant force increased?

 

[EnricoHendro]

I believe that your logic is correct regarding response to d).

This cube is submerged in two different fluids; therefore, it is displacing two volumes of different densities.
The addition of those two weights must be equal to the 75 N of buoyant force.

Consider the profile of pressure distribution for water only, for response to b).
Then, consider the different profiles of pressure distribution for both fluids as submerged depth increases.

Please, see:
https://courses.lumenlearning.com/boundless-physics/chapter/archimedes-principle/

Thank you, will check that link out to sharpen my understanding of the concept

 

[EnricoHendro]

Part D is correct, except that you seem to have changed the meaning of B after the first line.

You have not really finished part C. As you say, the tension increases, but you are asked to explain why.
Given that forces the oil exerts directly on the block are horizontal, why has the buoyant force increased?

oh I see. Yeah, I got my explanation all over the place. I was considering the density of the block being less than that of the oil, and I thought, if the object has density less of that of a fluid then it would start floating. I think I used the wrong logic for part C, as you've pointed out, I did stated that the oil exerts force inwards, so I still have to think of a better and correct explanation for part C. Thank you for pointing this out though.

For part D, yeah I took B as the combined buoyancy due to different fluids the block is subjected to. I think I have to revisit the concept as it is clear that I still haven't fully grasp the concept correctly.

 

[EnricoHendro]

I believe that your logic is correct regarding response to d).

This cube is submerged in two different fluids; therefore, it is displacing two volumes of different densities.
The addition of those two weights must be equal to the 75 N of buoyant force.

Consider the profile of pressure distribution for water only, for response to b).
Then, consider the different profiles of pressure distribution for both fluids as submerged depth increases.

Please, see:
https://courses.lumenlearning.com/boundless-physics/chapter/archimedes-principle/

wait a minute, don't you mean the addition of those two weights must be equal to the 25 N of the buoyant force?

 

[Lnewqban]

wait a minute, don't you mean the addition of those two weights must be equal to the 25 N of the buoyant force?

When the amount of oil that you have correctly calculated is added, the string breaks.
According to your equation, down-pulling tension of the string is 60 N, down-pulling gravity force is 15 N; therefore, the up-pushing buoyant force should be 75 N.
The block is anchored to the bottom of the beaker; because of that, as the level of the fluid increases, the block is forced to displace more and more volume of fluid, more than it would need to naturally float freely.

 

[EnricoHendro]

When the amount of oil that you have correctly calculated is added, the string breaks.
According to your equation, down-pulling tension of the string is 60 N, down-pulling gravity force is 15 N; therefore, the up-pushing buoyant force should be 75 N.
The block is anchored to the bottom of the beaker; because of that, as the level of the fluid increases, the block is forced to displace more and more volume of fluid, more than it would need to naturally float freely.

oh yeah, according to my equation the up pushing buoyant should be 75N. my bad, didn't pay enough attention to my own equation.

 

[Lnewqban]

It is important for your full understanding that you try to respond the question of @haruspex in post #5 above.
Again, the modified pressure distribution around the block that the additional oil creates is key for answering his question.

 

[EnricoHendro]

Part D is correct, except that you seem to have changed the meaning of B after the first line.

You have not really finished part C. As you say, the tension increases, but you are asked to explain why.
Given that the forces the oil exerts directly on the block are horizontal, why has the buoyant force increased?

Hello there Mr. Haruspex,
regarding your question on why has the buoyant force increased, is it correct to say "since the oil exerts inward force on each of the 4 side walls, therefore, the oil does not exert a downward force on the object as it is not "pushing" or exerting any pressure on top of the object. Since the oil is on top of the water, the oil exerts pressure on the water, and this pressure is distributed undiminished according to the pascal's law. This in turn increases the upward pressure of the water, which in turn increases the upward force exerted on the object. Since buoyant force is a resultant force exerted by the liquid surrounding the object, and given that the top side of the object is still exposed to the atmospheric pressure, the buoyant force exerted on the object increases." ?

 

[haruspex]

Hello there Mr. Haruspex,
regarding your question on why has the buoyant force increased, is it correct to say "since the oil exerts inward force on each of the 4 side walls, therefore, the oil does not exert a downward force on the object as it is not "pushing" or exerting any pressure on top of the object. Since the oil is on top of the water, the oil exerts pressure on the water, and this pressure is distributed undiminished according to the pascal's law. This in turn increases the upward pressure of the water, which in turn increases the upward force exerted on the object. Since buoyant force is a resultant force exerted by the liquid surrounding the object, and given that the top side of the object is still exposed to the atmospheric pressure, the buoyant force exerted on the object increases." ?

Yes, that's it. But for the purposes of the question it should be enough to say "the oil exerts pressure on the water. This increases the pressure of the water at all depths, which in turn increases the upward force exerted on the object."

 

[EnricoHendro]

Yes, that's it. But for the purposes of the question it should be enough to say "the oil exerts pressure on the water. This increases the pressure of the water at all depths, which in turn increases the upward force exerted on the object."

I understand now, Thank you for your help, really appreciate it